Обратни тригонометрични функции

Обрàтните тригонометрѝчни фу̀нкции, наричани още àркусфункции или циклометрѝчни функции, се дефинират като обратни на тригонометричните функции. Те определят ъгъла, съответстващ на дадена отсечка в единичната окръжност. Това са функциите:

За окръжност с радиус 1, $\arcsin {x}$ и $\arccos {y}$ e дъгата, определена от точката с координати $x$ и $y$ или ъгълът срещу нея.

• Аркуссинус $y=\arcsin {x}$, обратна на синус $x=\sin {y}$;
• Аркускосинус $y=\arccos {x}$, обратна на косинус $x=\cos {y}$;
• Аркустангeнс $y=\operatorname {arctg} {x}$, обратна на тангeнс $x=\operatorname {tg} {y}$;
• Аркускотангeнс $y=\operatorname {arccotg} {x}$, обратна на котангeнс $x=\operatorname {cotg} {y}$;
• Аркуссеканс $y=\operatorname {arcsec} {x}$, обратна на секанс $x=\sec {y}$;
• Аркускосеканс $y=\operatorname {arccsc} {x}$, обратна на косеканс $x=\csc {y}$.

Обратните тригонометрични функции служат за намиране на ъгъл от която и да е от неговите тригонометрични функции, но също и за обяснение на антипроизводните (първообразите, примитивите) на определени функции. Те се използват широко в инженерството, навигацията, физиката и геометрията.

Аркусфункциите са многозначни, защото съответните им тригонометрични функции са периодични. Стойността на аркусфункцията е множество от ъгли (дъги), за които съответната права тригонометрична функция е равна на даденото число. Например $\arcsin 1/2$ означава множеството от ъгли $\left({\frac {\pi }{6}},{\frac {5\pi }{6}},{\frac {13\pi }{6}},{\frac {17\pi }{6}}\dots ~(30^{\circ },150^{\circ },390^{\circ },510^{\circ }\dots )\right)$, синусът от които е $1/2$. От множеството от стойности на всяка аркусфункция се отделят нейните главни стойности (вижте графиките на главните стойности на аркусфункциите по-долу), които обикновено се имат предвид, когато се говори за тази аркусфункция. В примера главната стойност на $\arcsin 1/2$ е ${\frac {\pi }{6}}\,(30^{\circ })$.

Означения и имена

Обратните тригонометрични функции се означават със стандартен или съкратен запис на името им или чрез правата им функция:

Означения на обратните тригонометрични функции

Функция	Стандартни	Съкратени	С правата функция	Произношение
Аркуссинус	$\arcsin {x}$ $\arcsin(x)$	$\operatorname {asin} {x}$ $\operatorname {asin} (x)$	${\sin }^{-1}x$ ${\sin }^{-1}(x)$	аркуссинус от хикс
Аркускосинус	$\arccos {x}$ $\arccos(x)$	$\operatorname {acos} {x}$ $\operatorname {acos} (x)$	${\cos }^{-1}x$ ${\cos }^{-1}(x)$	аркускосинус от хикс
Аркустангeнс	$\operatorname {arctg} {x}$ $\operatorname {arctg} (x)$ $\arctan {x}$ $\arctan(x)$	$\operatorname {atg} {x}$ $\operatorname {atg} (x)$ $\operatorname {atan} {x}$ $\operatorname {atan} (x)$	${\operatorname {tg} }^{-1}x$ ${\operatorname {tg} }^{-1}(x)$ ${\tan }^{-1}x$ ${\tan }^{-1}(x)$	аркустангeнс от хикс
Аркускотангeнс	$\operatorname {arccot} {x}$ $\operatorname {arccot}(x)$ $\operatorname {arccotg} {x}$ $\operatorname {arccotg} (x)$ $\operatorname {arcctg} {x}$ $\operatorname {arcctg} (x)$	$\operatorname {acot} {x}$ $\operatorname {acot} (x)$ $\operatorname {acotg} {x}$ $\operatorname {acotg} (x)$ $\operatorname {actg} {x}$ $\operatorname {actg} (x)$	${\cot }^{-1}x$ ${\cot }^{-1}(x)$ ${\operatorname {cotg} }^{-1}x$ ${\operatorname {cotg} }^{-1}(x)$ ${\operatorname {ctg} }^{-1}x$ ${\operatorname {ctg} }^{-1}(x)$	аркускотангенс от хикс
Аркуссеканс	$\operatorname {arcsec} {x}$ $\operatorname {arcsec}(x)$	$\operatorname {asin} {x}$ $\operatorname {asec} (x)$	${\sec }^{-1}x$ ${\sec }^{-1}(x)$	аркусеканс от хикс
Аркускосеканс	$\operatorname {arccsc} {x}$ $\operatorname {arccsc}(x)$	$\operatorname {acsc} {x}$ $\operatorname {acsc} (x)$	${\csc }^{-1}x$ ${\csc }^{-1}(x)$	аркускосеканс от хикс

В езиците за компютърно програмиране обратните тригонометрични функции обикновено се означават ​​със съкратените форми Asin, Acos и Atan (във Visual Basic); ​ asin, acos и atan (в C++);​ или ArcSin, ArcCos и ArcTan (в Паскал).

Името на обратната тригонометрична функция се формира от името на съответната права тригонометрична функция чрез добавяне на префикса „aркус-“ (от латински arcus – дъга). Това се дължи на факта, че геометрично стойността на обратната тригонометрична функция може да бъде свързана с дължината на дъгата на единичната окръжност (или ъгъла, обхващащ тази дъга), съответстваща на определен сегмент. По този начин обикновеният синус позволява да се намери хорда, която го свързва по дъга от окръжност, а обратната функция решава обратния проблем. Начинът за обозначаване на обратните тригонометрични функции по този начин се появява при австрийския математик от 18 век Карл Шерфер и е установен благодарение на Лагранж. Специалният символ за обратната тригонометрична функция е използван за първи път от Даниел Бернули през 1729 г. До края на 19 век английската и немската математически школи предлагат други обозначения: $\sin ^{-1},{\frac {1}{\sin }}$, но те не се утвърждават. Само понякога в чуждестранната литература, както и в научни/инженерни калкулатори, се използват обозначения като sin⁻¹, cos⁻¹ за аркуссинус, аркускосинус и т.н. – такова обозначение се счита за не много удобно, тъй като е възможно объркване с функцията, повдигната на степен −1. Объркването се смекчава донякъде от факта, че всяка от реципрочните тригонометрични функции има собствено име, например (cos(x))⁻¹ = sec(x). Предпочита се обаче такова обозначение да не се използва поради неговата двусмисленост.​ Друг вариант, използван от някои автори, е означение с първа главна буква, заедно с горен индекс ⁻¹: Sin⁻¹(x), Cos⁻¹(x ), Tan⁻¹(x) и т.н. Това потенциално избягва объркване със съответната обратна функция, която трябва да бъде представена чрез sin⁻¹(x), cos⁻¹(x) ... или по-добре чрез sin⁻¹ x, cos⁻¹ x и т.н. Обаче се създава още един основен източник на неяснота, особено след като много популярни езици за програмиране на високо ниво (напр. Mathematica и Magma) използват същите тези представяния с главни букви за стандартните тригонометрични функции, докато други (Python, SymPy, NumPy, MATLAB, Maple и др.) използват малки букви.

От 2009 г. насам стандартът ISO 80000-2 уточнява само префикса „arc“ за обратните функции.

Основни съотношения

Удовлетворени са зависимостите:

$\arcsin {\sin {x}}=\sin {\arcsin {x}}=x$

$\arccos {\cos {x}}=\cos {\arccos {x}}=x$

$\arctan {\tan {x}}=\tan {\arctan {x}}=x$

$\operatorname {arccot} {\cot {x}}=\cot {\operatorname {arccot} {x}}=x$

$\arcsin {\sec {x}}=\sin {\arcsin {x}}=x$

$\arccos {\csc {x}}=\cos {\arccos {x}}=x$

$\arcsin x+\arccos x={\frac {\pi }{2}}$

$\operatorname {arctg} \,x+\operatorname {arcctg} \,x={\frac {\pi }{2}}$

Функция arcsin

Аркусинус на числото x е стойността на ъгъла y, изразена в радиани, за която $\sin y=x,\quad -{\frac {\pi }{2}}\leqslant y\leqslant {\frac {\pi }{2}},\quad |x|\leqslant 1.$

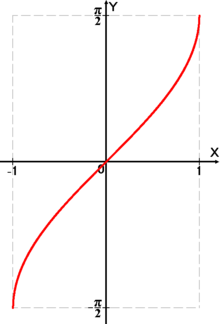
Графика на функцията $y=\arcsin x$

Функцията $y=\arcsin x$ е непрекъсната и ограничена в цялата си дефиниционна област. Тя е строго нарастваща.

• $\sin(\arcsin x)=x\qquad$ при $-1\leqslant x\leqslant 1,$
• $\arcsin(\sin y)=y\qquad$ за $-{\frac {\pi }{2}}\leqslant y\leqslant {\frac {\pi }{2}},$
• Дефиниционна област $\qquad D(\arcsin x)=[-1;1]$,
• Област на стойностите $\qquad E(\arcsin x)=\left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]$.

Свойства на функцията arcsin

• $\arcsin(-x)=-\arcsin x\qquad$ (функцията е нечетна).
• $\arcsin x>0$ за $0<x\leqslant 1$.
• $\arcsin x=0$ за $x=0.$
• $\arcsin x<0$ за $-1\leqslant x<0.$
• $\arcsin x={\frac {\pi }{2}}-\arccos x.$
• $\arcsin x=\left\{{\begin{matrix}\arccos {\sqrt {1-x^{2}}},\qquad 0\leqslant x\leqslant 1\\-\arccos {\sqrt {1-x^{2}}},\qquad -1\leqslant x\leqslant 0\end{matrix}}\right.$
• $\arcsin x=\operatorname {arctg} {\frac {x}{\sqrt {1-x^{2}}}}$
• $\arcsin x=\left\{{\begin{matrix}\operatorname {arcctg} \,{\frac {\sqrt {1-x^{2}}}{x}},\qquad 0<x\leqslant 1\\\operatorname {arcctg} \,{\frac {\sqrt {1-x^{2}}}{x}}-\pi ,\qquad -1\leqslant x<0\end{matrix}}\right.$

Получаване на функцията arcsin

Дадена е функцията $y=\sin x$. В цялата си област на определяне тя е частично монотонна, следователно обратното съответствие $y=\arcsin x$ не е изпълнено по цялата числова линия. Затова се разглежда интервала $[-\pi /2;\pi /2]$, в който функцията $y=\sin x$ строго монотонно нараства и приема всички свои стойности само веднъж. Тогава в интервала $[-\pi /2;\pi /2]$ съществува обратната функция $y=\arcsin x$, чиято графика е симетрична на графиката на функцията $y=\sin x$ относно правата $y=x$.

Функция arccos

Аркускосинус на числото x се нарича такава стойност на ъгъла y, изразена в радиани, за която

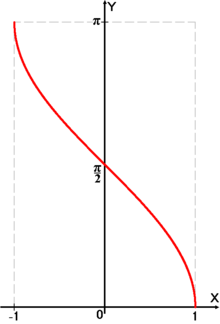
Графика на функцията $y=\arccos x$

$\cos y=x,\qquad 0\leqslant y\leqslant \pi ,\quad |x|\leqslant 1.$

Функцията $y=\arccos x$ е непрекъсната и ограничена в цялата си дефиниционна област. Тя е строго намаляваща и неотрицателна.

• $\cos(\arccos x)=x$ при $-1\leqslant x\leqslant 1,$
• $\arccos(\cos y)=y$ при $0\leqslant y\leqslant \pi .$
• Дефиниционна област $\qquad D(\arccos x)=[-1;1]$,
• Област на стойностите $\qquad E(\arccos x)=[0;\pi ]$.

Свойства на функцията arccos

• $\arccos(-x)=\pi -\arccos x.$ Функцията е централно симетрична по отношение на точката $\left(0;{\frac {\pi }{2}}\right),$ тя е индиферентна (нито четна, нито нечетна).
• $\arccos x>0$ при $-1\leqslant x<1.$
• $\arccos x=0$ при $x=1.$
• $\arccos x={\frac {\pi }{2}}-\arcsin x.$
• $\arccos x=\left\{{\begin{matrix}\arcsin {\sqrt {1-x^{2}}},\qquad 0\leqslant x\leqslant 1\\\pi -\arcsin {\sqrt {1-x^{2}}},\qquad -1\leqslant x\leqslant 0\end{matrix}}\right.$
• $\arccos x=\operatorname {arcctg} {\frac {x}{\sqrt {1-x^{2}}}}$
• $\arccos x=\left\{{\begin{matrix}\operatorname {arctg} \,{\frac {\sqrt {1-x^{2}}}{x}},\qquad 0<x\leqslant 1\\\pi +\operatorname {arctg} \,{\frac {\sqrt {1-x^{2}}}{x}},\qquad -1\leqslant x<0\end{matrix}}\right.$
• $\arccos x=2\arcsin {\sqrt {\frac {1-x}{2}}}$
• $\arccos x=2\arccos {\sqrt {\frac {1+x}{2}}}$
• $\arccos x=2\operatorname {arctg} {\sqrt {\frac {1-x}{1+x}}}=2\operatorname {arctg} {\frac {\sqrt {1-x^{2}}}{1+x}}$

Получаване на функцията arccos

Дадена е функцията $y=\cos x$. В цялата си дефиниционна област тя е частично монотонна, следователно обратното съответствие $y=\arccos x$ не е изпълнено по цялата числова линия. Затова се разглежда интервала $[0;\pi ]$, в който функцията $y=\cos x$ строго монотонно намалява и приема всички свои стойности само веднъж. Тогава в интервала $[0;\pi ]$ съществува обратната функция $y=\arccos x$, чиято графика е симетрична на графиката на функцията $y=\cos x$ относно правата $y=x$.

Функция arctg

Аркустангенс на числото x се нарича такава стойност на ъгъла $y,$ изразена в радиани, за която

Графика на функцията $y=\operatorname {arctg} \,x$

$\operatorname {tg} y=x,\quad -{\frac {\pi }{2}}<y<{\frac {\pi }{2}}.$

Функцията $y=\operatorname {arctg} x$ е определена по цялата числова линия, навсякъде непрекъсната и ограничена. Тя е строго нарастваща.

• $\operatorname {tg} \,(\operatorname {arctg} \,x)=x$ при $x\in \mathbb {R} ,$
• $\operatorname {arctg} x=\left\{{\begin{matrix}\operatorname {arcctg} {\frac {1}{x}},\qquad x>0\\\operatorname {arcctg} {\frac {1}{x}}-\pi ,\qquad x<0\end{matrix}}\right.$
• Дефиниционна област $\qquad D(\operatorname {arctg} \,x)=(-\infty ;\infty )$.
• Област на стойностите $\qquad E(\operatorname {arctg} \,x)=\left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right)$.

Свойства на функцията arctg

• $\operatorname {arctg} (-x)=-\operatorname {arctg} x\qquad$ (функцията е нечетна).
• $\operatorname {arctg} x=\arcsin {\frac {x}{\sqrt {1+x^{2}}}}$.
• $\operatorname {arctg} x=\left\{{\begin{matrix}\arccos {\frac {1}{\sqrt {1+x^{2}}}},\qquad x\geqslant 0\\-\arccos {\frac {1}{\sqrt {1+x^{2}}}},\qquad x\leqslant 0\end{matrix}}\right.$
• $\operatorname {arctg} x=2\operatorname {arctg} {\frac {x}{{\sqrt {1+x^{2}}}+1}}=2\operatorname {arctg} {\frac {{\sqrt {1+x^{2}}}-1}{x}}$.
• $\operatorname {arctg} x=\pi /2-\operatorname {arcctg} x$.
• $\operatorname {arctg} x=\left\{{\begin{matrix}\operatorname {arcctg} {\frac {1}{x}},\qquad x>0\\\operatorname {arcctg} {\frac {1}{x}}-\pi ,\qquad x<0\end{matrix}}\right.$
• $\operatorname {arctg} x=-i\operatorname {arth} {ix}$, където $\operatorname {arth}$ е обратен хиперболичен тангенс, ареатангенс.
• $\operatorname {arth} x=i\operatorname {arctg} {ix}.$

Получаване на функцията arctg

Дадена е функцията $y=\operatorname {tg} \,x$. В цялата си дефиниционна област тя е частично монотонна, следователно обратното съответствие $y=\operatorname {arctg} \,x$ на функцията не е изпълнено. Затова се разглежда интервала $(-\pi /2;\pi /2)$, в който функцията $y=\operatorname {tg} \,x$ строго монотонно нараства и приема всички стойности от своята област на стойностите само веднъж. Тогава в интервала $(-\pi /2;\pi /2)$ съществува обратната функция $y=\operatorname {arctg} \,x$, чиято графика е симетрична на графиката на функцията $y=\operatorname {tg} \,x$ относно правата $y=x$.

Функция arcctg

Графика на функцията $y=\operatorname {arcctg} x$

Аркустангенс на числото x е стойността на ъгъла y (в радиани), за който $\operatorname {ctg} \,y=x,\quad 0<y<\pi .$

Функцията $y=\operatorname {arcctg} \,x$ е дефинирана на цялата числова ос, непрекъсната е и ограничена навсякъде. Тя е строго намаляваща и положителна навсякъде.

• $\operatorname {ctg} (\operatorname {arcctg} \,x)=x$ за $x\in \mathbb {R} ,$
• $\operatorname {arcctg} (\operatorname {ctg} \,y)=y$ за $0<y<\pi ,$
• Дефиниционна област $\qquad D(\operatorname {arcctg} x)=(-\infty ;\infty ),$
• Област на стойностите $\qquad E(\operatorname {arcctg} x)=(0;\pi ).$

Свойства на функцията arcctg

• $\operatorname {arcctg} (-x)=\pi -\operatorname {arcctg} x.$ Графиката на функцията е централно симетрична спрямо точката $\left(0;{\frac {\pi }{2}}\right).$ Функцията е безразлична (нито четна, нито нечетна).
• $\operatorname {arcctg} x>0$ за всеки $x.$
• $\operatorname {arcctg} x=\arccos {\frac {x}{\sqrt {1+x^{2}}}}.$
• $\operatorname {arcctg} x=\left\{{\begin{matrix}\arcsin {\frac {1}{\sqrt {1+x^{2}}}},\qquad x\geqslant 0\\\pi -\arcsin {\frac {1}{\sqrt {1+x^{2}}}},\qquad x\leqslant 0\end{matrix}}\right.$
• $\operatorname {arcctg} x=2\operatorname {arctg} ({\sqrt {x^{2}+1}}-x)=2\operatorname {arcctg} ({\sqrt {x^{2}+1}}+x).$
• $\operatorname {arcctg} x=\pi /2-\operatorname {arctg} x.$
• $\operatorname {arcctg} x=\left\{{\begin{matrix}\operatorname {arctg} {\frac {1}{x}},\qquad x>0\\\operatorname {arctg} {\frac {1}{x}}+\pi ,\qquad x<0\end{matrix}}\right.$

Получаване на функция arcctg

Дадена е функцията $y=\operatorname {ctg} \,x$. В цялата си дефиниционна област тя е частично монотонна и следователно обратното съответствие $y=\operatorname {arcctg} \,x$ не съществува. Затова се разглежда интервала $(0;\pi )$, в който функцията $y=\operatorname {ctg} \,x$ строго монотонно намалява и приема всички стойности от своята област само веднъж. Тогава в интервала $(0;\pi )$ съществува обратна функция $y=\operatorname {arcctg} \,x$, чиято графика е симетрична на графиката на функцията $y=\operatorname {ctg} \,x$ спрямо правата $y=x$.

Графиката на функцятаАркускоотангенсна се получава от аркустангенсната графика, ако последната е отразена спрямо ординатната ос (т.е. сменяйки знака на аргумента, $x\rightarrow -x$) и е изместена нагоре с π/2; това следва от горната формула $\operatorname {arcctg} x=\operatorname {arctg} (-x)+\pi /2.$

Функция arcsec

Аркуссеканс на числото $x$ е стойността на ъгъла $y$ (в радиани), за която

Графика на функцията $y=\operatorname {arcsec} \,x$

$\sec y=x,\qquad |x|\geqslant 1,\quad 0\leqslant y\leqslant \pi$.

Функцията $y=\operatorname {arcsec} x$ е непрекъсната и ограничена в цялата си дефиниционна област. Тя е строго нарастваща и неотрицателна навсякъде.

• $\sec(\operatorname {arcsec} x)=x$ при $|x|\geqslant 1,$
• $\operatorname {arcsec}(\sec y)=y$ при $0\leqslant y\leqslant \pi .$
• Дефиниционна област

$D(\operatorname {arcsec} x)=(-\infty ;-1]\cup [1,\infty )$

• Област на стойностите

$E(\operatorname {arcsec} x)=[0;{\frac {\pi }{2}})\cup ({\frac {\pi }{2}};\pi ]$.

Свойства на функцията arcsec

• $\operatorname {arcsec}(-x)=\pi -\operatorname {arcsec} x.$ Графиката на функцията е централно симетрична спрямо точката $\left(0;{\frac {\pi }{2}}\right).$ Функцията е индиферентна (нито четна, нито нечетна).
• $\operatorname {arcsec} x\geqslant 0$ за всички $x.$
• $\operatorname {arcsec} x=\left\{{\begin{matrix}\arcsin {\frac {\sqrt {x^{2}-1}}{x}},\qquad x\geqslant 1\\\pi +\arcsin {\frac {\sqrt {x^{2}-1}}{x}},\qquad x\leqslant -1\end{matrix}}\right.$
• $\operatorname {arcsec} x={\frac {\pi }{2}}-\operatorname {arccosec} x.$
• $\operatorname {arcsec} x=\arccos {\frac {1}{x}}.$

Функция arccosec

Аркосеканс на числото x е стойността на ъгъла y (в радиани), за която

Графика на функцията $y=\operatorname {arccosec} x$

$\operatorname {cosec} y=x$, $|x|\geqslant 1,\quad -\pi /2\leqslant y\leqslant \pi /2.$

Функцията $\,y=\operatorname {arccosec} x\,$ е непрекъсната и ограничена в цялата си област на определение. Тя е строго намаляваща.

• $\operatorname {cosec} (\operatorname {arccosec} x)=x$ при $|x|\geqslant 1,$
• $\operatorname {arccosec} (\operatorname {cosec} y)=y$ при $-\pi /2\leqslant y\leqslant \pi /2.$
• Дефиниционна област $D(\operatorname {arccosec} x)=(-\infty ;-1]\cup [1,\infty )$,
• Област на стойностите $\quad E(\operatorname {arccosec} x)=[-{\frac {\pi }{2}};0)\cup (0;{\frac {\pi }{2}}]$.

Свойства на функцията arccosec

• $\operatorname {arccosec} (-x)=-\operatorname {arccosec} x$ (функцията е нечетна).
• $\operatorname {arccosec} \,x=\operatorname {arctg} {\frac {\operatorname {sgn} x}{\sqrt {x^{2}-1}}}=\left\{{\begin{matrix}\operatorname {arctg} {\frac {1}{\sqrt {x^{2}-1}}},\qquad x>1\\-\operatorname {arctg} {\frac {1}{\sqrt {x^{2}-1}}},\qquad x<-1\end{matrix}}\right.$
• $\operatorname {arccosec} x=\pi /2-\operatorname {arcsec} x.$
• $\operatorname {arccosec} x=\arcsin {\frac {1}{x}}.$

Сравнение и обобщение

Основните стойности на функциите $\arcsin {(x)}$ (червено) и $\arccos {(x)}$ (синьо)	Основните стойности на функциите $\arctan {(x)}$ (червено) и $\operatorname {arccot} {(x)}$ (синьо)
	Основните стойности на функциите $\operatorname {arcsec} {(x)}$ (червено) и $\operatorname {arccsc} {(x)}$ (синьо)

Риманова повърхност на комплексен логаритъм. Листите са на разстояние $2\pi$.

Тъй като тригонометричните функции са периодични функции, те първоначално не са обратими. Ако обаче се ограничи до интервал на монотонност на съответната изходна функция, например интервала $[-\pi /2,\pi /2]$ или $[0,\pi ]$, тогава ограничената функция, получена по този начин, може много добре да бъде обърната. Въпреки това, интервалите на монотонност покриват само половин период, както се вижда от графиките на функциите. Въпреки това, ако се знае както синуса, така и косинуса на ъгъл, можете да се определи ъгъла до цели периоди $(2\pi )$, (вижте фигурата на вдясно за илюстрация и atan2 за изчисление).

Връзки между функциите

Вижте също: Тригонометрична функция: връзки между функциите

Aркусфункциите могат да бъдат преобразувани една в друга, както следва ($\operatorname {sgn}$ обозначава знаковата функция):

	arcsin	arccos	arctan	arccot	arcsec	arccsc
arcsin(x)	$\arcsin(x)$	${\frac {\pi }{2}}-\arccos(x)$	$\arctan \left({\frac {x}{\sqrt {1-x^{2}}}}\right)$	${\frac {\pi }{2}}-\operatorname {arccot} \left({\frac {x}{\sqrt {1-x^{2}}}}\right)$	${\frac {\pi }{2}}-\operatorname {arcsec} \left({\frac {1}{x}}\right)$	$\operatorname {arccsc} \left({\frac {1}{x}}\right)$
arccos(x)	${\frac {\pi }{2}}-\arcsin(x)$	$\arccos(x)$	${\frac {\pi }{2}}-\arctan \left({\frac {x}{\sqrt {1-x^{2}}}}\right)$	$\operatorname {arccot} \left({\frac {x}{\sqrt {1-x^{2}}}}\right)$	$\operatorname {arcsec} \left({\frac {1}{x}}\right)$	${\frac {\pi }{2}}-\operatorname {arccsc} \left({\frac {1}{x}}\right)$
arctan(x)	$\arcsin \left({\frac {x}{\sqrt {1+x^{2}}}}\right)$	${\frac {\pi }{2}}-\arccos \left({\frac {x}{\sqrt {1+x^{2}}}}\right)$	$\arctan(x)$	${\frac {\pi }{2}}-\operatorname {arccot}(x)$	${\frac {\pi }{2}}-\operatorname {arcsec} \left({\frac {\sqrt {1+x^{2}}}{x}}\right)$	$\operatorname {arccsc} \left({\frac {\sqrt {1+x^{2}}}{x}}\right)$
arccot(x)	${\frac {\pi }{2}}-\arcsin \left({\frac {x}{\sqrt {1+x^{2}}}}\right)$	$\arccos \left({\frac {x}{\sqrt {1+x^{2}}}}\right)$	${\frac {\pi }{2}}-\arctan(x)$	$\operatorname {arccot}(x)$	$\operatorname {arcsec} \left({\frac {\sqrt {1+x^{2}}}{x}}\right)$	${\frac {\pi }{2}}-\operatorname {arccsc} \left({\frac {\sqrt {1+x^{2}}}{x}}\right)$
arcsec(x)	${\frac {\pi }{2}}-\arcsin \left({\frac {1}{x}}\right)$	$\arccos \left({\frac {1}{x}}\right)$	${\frac {\pi }{2}}-\arctan \left({\frac {\operatorname {sgn}(x)}{\sqrt {x^{2}-1}}}\right)$	$\operatorname {arccot} \left({\frac {\operatorname {sgn}(x)}{\sqrt {x^{2}-1}}}\right)$	$\operatorname {arcsec}(x)$	${\frac {\pi }{2}}-\operatorname {arccsc}(x)$
arccsc(x)	$\arcsin \left({\frac {1}{x}}\right)$	${\frac {\pi }{2}}-\arccos \left({\frac {1}{x}}\right)$	$\arctan \left({\frac {\operatorname {sgn}(x)}{\sqrt {x^{2}-1}}}\right)$	${\frac {\pi }{2}}-\operatorname {arccot} \left({\frac {\operatorname {sgn}(x)}{\sqrt {x^{2}-1}}}\right)$	${\frac {\pi }{2}}-\operatorname {arcsec}(x)$	$\operatorname {arccsc}(x)$

Разложение в редове

• $\displaystyle \arcsin x=x+{\frac {x^{3}}{6}}+{\frac {3x^{5}}{40}}+\cdots \ =\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}$ за всички $\left|x\right|\leq 1$
• $\displaystyle \arccos x={\pi \over 2}-\arcsin x={\pi \over 2}-\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}$ за всички $\left|x\right|\leq 1$
• $\displaystyle \operatorname {arctg} \ x=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-\cdots \ =\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}}{2n-1}}x^{2n-1}$ за всички $\left|x\right|\leq 1$

Вижте още

• Обратни хиперболични функции