Гравитация

Серия статии на тема Класическа механика

Импулс  · Сила  · Енергия  · Работа  · Мощност  · Скорост  · Ускорение  · Инерционен момент  · Момент на сила  · Момент на импулса Основни понятия Пространство  · Време  · Маса  · Тегло  · Гравитация Формулировки Нютонова механика  · Механика на Лагранж  · Хамилтонова механика  · Раздели Кинематика  · Динамика  · Приложна механика  · Небесна механика  · Статистическа механика  · Механика на флуидите Закони за запазване Закон за запазване на механичната енергия  · Закон за запазване на импулса  · Закон за запазване на момента на импулса Учени Галилео Галилей  · Йохан Кеплер Исак Нютон  · Леонард Ойлер Пиер-Симон Лаплас  · Жан Лерон д'Аламбер Жозеф Луи Лагранж  · Уилям Роуън Хамилтон Огюстен Луи Коши

Гравитацията (също гравитационно взаимодействие, всемирно привличане, универсално притегляне; от латински: gravitas – „тежест“) е природно явление, в резултат на което всички обекти, притежаващи маса или енергия – включително планети, звезди, галактики и дори светлината – се привличат (или гравитират) един към друг.

На Земята гравитацията придава тегло на физичните обекти, а лунната гравитация причинява приливите и отливите. Гравитационното привличане на първоначалната газообразна материя във Вселената я кара да коалесцира, образувайки звезди, а звездите от своя страна се групират заедно в галактики, като по този начин на гравитацията се дължат много от едромащабните структури на Вселената. Гравитацията има неограничен обхват, но нейните ефекти стават все по-слаби с отдалечаването на обектите един от друг.

Гравитацията е най-точно описана от общата теория на относителността (предложена от Алберт Айнщайн през 1915 година), която я разглежда не като сила, а като последица от изкривяване на пространство-времето, причинено от неравномерното разпределение на масата. Най-яркият пример за това изкривяване е черната дупка, която нищо, дори и светлина, не може да напусне, след като премине отвъд нейния хоризонт на събитията. При повечето приложения обаче гравитацията с добро приближение следва закона за всеобщото привличане на Исак Нютон, който я описва като сила, която кара всеки две тела да се привличат едно към друго и която е пропорционална на произведението на техните маси и обратно пропорционална на квадрата на разстоянието между тях.

Гравитацията е най-слабото от четирите фундаментални взаимодействия във физиката, приблизително 10³⁸ пъти по-слаба от силното, 10³⁶ пъти по-слаба от електромагнитното и 10²⁹ пъти по-слаба от слабото взаимодействие. Вследствие на това тя няма съществено влияние на ниво субатомни частици. Обратно, при едромащабните явления гравитацията е преобладаващото взаимодействие и е причина за възникването, оформянето и траекториите на астрономическите тела.

Първата проява на гравитация във Вселената, може би под формата на квантова гравитация, супергравитация или гравитационна сингулярност, се развива, заедно с обикновеното пространство и време, в Епохата на Планк (до 10⁻⁴³ секунди след появата на Вселената) по неизвестен днес начин от предходно състояние като лъжлив вакуум, квантов вакуум или виртуална частица. Съвременните изследвания са насочени към създаване на теория на гравитацията, съвместима с квантовата механика – теория на квантовата гравитация, – която би позволила гравитацията и останалите фундаментални взаимодействия да се обединят в обща математическа рамка (теория на всичко).

Общи характеристики

Класическа гравитационна теория

В класическата механика гравитационното взаимодействие се изразява с формулата за гравитационната сила:

$F=G{\frac {m_{1}m_{2}}{r^{2}}},$

където:

• F е силата на привличане между двата взаимодействащи си обекта,
• G е гравитационна константа, приблизително равна на 6,675⋅10⁻¹¹ m³/(kg·s²)
• m₁ е масата на единия обект,
• m₂ е масата на другия обект,
• r е разстоянието между центровете на масите на двата обекта.

Макар създадената в началото на XX век обща теория на относителността да дава по-общо и прецизно описание на гравитацията, класическата гравитационна теория продължава да си използва широко, заради своята простота и достатъчната си точност при скорости, много по-малки от скоростта на светлината ($v\ll c$), и относително малка маса $M$ на привличащото тяло (${\frac {GM}{c^{2}r}}\ll 1$).

Обща теория на относителността

Двуизмерно представяне на изкривяването на четириизмерното пространство-време, предизвиквано от масата на даден предмет: наличието на материя променя геометрията на пространство-времето и тази изкривена геометрия се интерпретира като гравитация; белите линии изобразяват не изкривяването на пространството, а координатна система, наложена върху изкривеното пространство-време, която би била ортогонална при плоско пространство-време

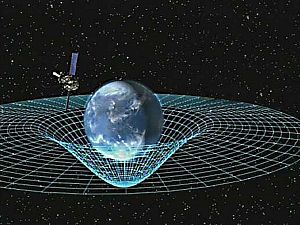
В повечето случаи, отнасящи се за слаби гравитационни полета (например изпращане на ракети до Луната или в Слънчевата система), формулата на Нютон е достатъчно точна. Според общата теория на относителността обаче вместо на някаква сила, ефектът на гравитацията се приписва на изкривяването на пространство-времето.

Изходна точка на общата теория на относителността е принципът на еквивалентността, който уеднаквява свободното падане с инерционното движение и описва свободно падащите инерционни обекти като ускорени спрямо неинерциалните наблюдатели на Земята. Проблемът, който изниква е, че свободно падащите тела се ускоряват и в Нютоновата физика такова ускорение може да се появи, само ако върху едно от телата действа сила (и следователно то не се движи по инерция).

За да се справи с тази пречка, Айнщайн предполага, че пространство-времето се изкривява от материята и свободно падащите тела се движат по локално прави пътища в изкривеното пространство-време. Тези прави пътища се наричат ​​геодезически. Подобно на първия закон за движението на Нютон, теорията на Айнщайн гласи, че ако се приложи сила върху обект, той ще се отклони от геодезическия път. Например, ние вече не следваме геодезическия път, докато стоим, защото механичното съпротивление на Земята упражнява върху нас насочена нагоре сила и в резултат на това не сме инерционни на земята. По този начин движението по геодезичните пътища в пространство-времето продължава да се смята за инерционно.

Айнщайн открива полевите уравнения на общата теория на относителността, които свързват присъствието на материята и кривината на пространство-времето и които са наречени на негово име. Уравненията на Айнщайн са система от 10 нелинейни диференциални уравнения. Решенията на тази система са компонентите на метричния тензор на пространство-времето. Даден метричен тензор описва геометрията на дадено пространство-време. Геодезичните пътища на дадено пространство-време се изчисляват чрез метричния тензор.

Принцип на еквивалентност

Принципът на еквивалентност, разглеждан през годините от изследователи, като Галилео Галилей, Лоранд Йотвьош и Алберт Айнщайн, изразява идеята, че всички предмети падат по един и същ начин и че ефектите на гравитацията са неразличими от определени страни на ускорението и забавянето.

Формулировките на принципа на еквивалентност включват:

• Слаб принцип на еквивалентност: Траекторията на материална точка в гравитационно поле зависи само от нейното начално положение и скорост и е независима от нейния състав.
• Айнщайнов принцип на еквивалентност: Резултатът от всеки локален негравитационен опит в свободно падаща лаборатория е независим от скоростта на лабораторията и нейното положение в пространство-времето.
• Силен принцип на еквивалентност: изискващ изпълнението на първите два принципа едновременно.

Най-простият начин за наблюдение на слабия принцип на еквивалентност е да се пуснат два предмета с различна маса или състав във вакуум и да се види дали паднат за едно и също време. Такива експерименти показват, че всички предмети падат с еднаква скорост, когато други сили, като съпротивлението на въздуха или електромагнитните въздействия, са пренебрежими. По усложнение опити използват торзионна везна, като изобретената от Йотвьош. За наблюдение на принципа на еквивалентност в космоса се използват прецизно планирани спътникови експерименти.

История на гравитационната теория

Водата във фонтана е илюстрация на гравитационната теория, според която струята трябва да описва парабола

Ранна история

От древни времена съществуват много опити да се разбере и обясни гравитационната сила. През 4 век пр.н.е. гръцкият философ Аристотел вярва, че няма ефект без причина и движение без сила. Според него причината за движението надолу на тежки тела, като елементът земя, е свързано с тяхната природа, което ги кара да се движат надолу към центъра на Вселената, което е тяхното естествено място. Обратно, леки тела като елементът огън се движат по своята същност нагоре към вътрешната повърхност на сферата на Луната. Така в системата на Аристотел тежките тела не са привлечени от Земята чрез външна сила на гравитацията, а са насочени към центъра на вселената поради вътрешни гравитати или тежести.

Древногръцкият изобретател Архимед открива центъра на тежестта на триъгълника. Той установява също, че ако две еднакви тежести нямат общ център на тежестта, общият им център на тежестта се намира по средата на линията, свързваща техните два центъра на тежестта. В книга VII на „За архитектурата“ римският инженер и архитект Витрувий твърди, че гравитацията не зависи от тежестта на веществото, а от неговата „природа“.

Индийският астроном Арябхата говори за сила, обясняваща защо обектите не са изхвърлени навън от въртенето на Земята. След него Брахмагупта описва гравитацията като привлекателна сила, която нарича с термина „гурутвакарсан“. Философът в древна Индия Канада, основателят на школата Вайшешика, се опитва да обясни гравитационната сила така: „Тежестта причинява падане, това е неосезаемо и се знае по подразбиране.“

Закон на Нютон за гравитацията

Съвременната, модерна трактовка на гравитацията започва с работите на Галилео Галилей в края на XVI век и началото на XVII век. Чрез известния си опит (макар и вероятно апокрифен) с падащи сферични тела от кулата в Пиза и по-късно с внимателни измервания на малки сфери, търкалящи се по наклонена равнина, Галилео показва, че земното ускорение е едно и също за всички тела. Това противоречи на вярванията на Аристотел, според когото по-тежките тела се ускоряват по-бързо (Галилей правилно посочва съпротивлението на въздуха като причината за впечатлението, че по-леките тела падат по-бавно). Работата на Галилео дава основите на формулирането на теорията на Нютон за гравитацията.

Гравитацията държи планетите от Слънчевата система в орбита около Слънцето

Първият математически модел, описващ гравитацията, е създаден от английския физик Исак Нютон и е изложен в публикувания от него през 1687 труд „Математически начала на натурфилософията“ („Philosophiæ Naturalis Principia Mathematica“), в който той излага хипотезата си, че всемирното привличане се подчинява на закон за обратните квадрати. По думите му: „Аз заключих, че силите, които придържат планетите към техните орбити, трябва да са реципрочни на квадратите на разстоянията им до центровете, около които се въртят – следователно аз сравних силата, нужна за да държи Луната в орбитата ѝ, с гравитационната сила на повърхността на Земята; и открих, че резултатите са доста близки.“ Идеята, че Слънцето действа на отдалечени обекти със сила, обратнопропорционална на квадрата на разстоянието до тях, е разглеждана още през 1645 година от французина Исмаел Булио, но той в крайна сметка отхвърля съществуването на такава сила.

Английският физик и математик Исак Нютон (1642 – 1727)

Макар законът на Нютон да описва коректно основните прояви на гравитацията, Исак Нютон не успява да създаде теория, която да обяснява кое причинява самото притегляне. Трудът му „Principia“ завършва с думите: „Досега аз изяснявах небесните явления и приливите на моретата на основание силите на привличане, но аз не посочих причините на самото притегляне. Тази сила произлиза от някаква причина, която прониква до центъра на Слънцето и планетите без намаляване на тази способност… като нейното действие се разпространява на огромни разстояния, намалявайки пропорционално на квадрата на разстоянието… Причината за тези свойства на силите на привличане аз досега не мога да изведа от явленията, а хипотези аз не измислям“.

Нютоновият закон се радва на най-големия си успех, след като предвижда съществуването на планетата Нептун, изхождайки от движението на Уран, което не би могло да се обясни чрез действията на другите планети. Пресмятанията и на Джон Кауч Адамс, и на Юрбен Льоверие, проведени през XIX век, предсказват приблизителното положение на планетата, а изчисленията на Льоверие довеждат до откриването на Нептун от Йохан Готфрид Гал.

Въпреки че Нютоновата теория е заменена от общата теория на относителността, и днес повечето нерелативистични гравитационни изчисления се основават на нея, тъй като тя е значително по-проста, а дава достатъчно точни резултати за повечето приложения, свързани с относително малки маси, скорости и енергии.

Релативистична теория на гравитацията

Създателят на общата теория на относителността Алберт Айнщайн (1879 – 1955)

По ирония на съдбата, въпреки ролята на откриването на Нептун за утвърждаването на Нютоновата гравитационна теория, аномалии в орбитата на друга планета, Меркурий, спомага за откриването на недостатъци в теорията на Нютон. В края на XIX век се знае, че орбитата на Меркурий има леки пертурбации – изместване на перихелия на планетата с 42,98 дъгови секунди напред на всяко столетие, – които не могат да се обяснят напълно чрез закона на Нютон, тъй като всички търсения на друго смущаващо орбитата тяло (като планета, обикаляща около Слънцето, по-близо дори от Меркурий) остават безплодни. Проблемът е разрешен през 1915 година от новата обща теория на относителността на Алберт Айнщайн, която обяснява нарушенията в орбитата на Меркурий.

Уравненията, дефинирани от Айнщайн, получават различни решения за частни случаи, най-известни сред които са:

• Решението на Шварцшилд, което описва пространство-времето около сферично симетричен невъртящ се електрически незареден масивен обект. За достатъчно компактни обекти, това решение води до извода за черна дупка с централна сингулярност. За радиални разстояния от нейния център, които са значително по-големи от радиуса на Шварцшилд, предвижданите от решението ускорения са практически равни на предвижданите от теорията на Нютон.
• Решението на Райснер Нордстрьом, което отчита и електрическия заряд на централния обект. При заряди с геометризирани дължини по-малки от геометризираната дължина на масата на обекта, това решение води до извода за черни дупки с двоен хоризонт на събитията.
• Решението на Кер отчита и въртенето на масивните обекти и също включва черни дупки с множество хоризонти на събитията.
• Решението на Кер-Нюман отчита едновременно и електрическия заряд, и въртенето на масивните обекти.
• Решението на Фридман-Льометр-Робъртсън-Уокър е използвано в космологията и описва разширението на Вселената.

Общата теория на относителността се потвърждава от поредица наблюдения на обяснявани от нея явления:

• Още със създаването си тя обяснява известната от по-рано прецесия на перихелия на Меркурий
• Отклоняването на светлината от гравитационно поле е наблюдавано от Артър Едингтън при слънчево затъмнение през 1919 година и потвърдено в началото на 70-те години с по-прецизни радиоинтерферометрични измервания на преминавания на квазари зад Слънцето
• През 20-те години Александър Фридман и Жорж Льометър стигат до извода, че уравненията на общата теория на относителността са несъвместими със статичен модел на Вселената и през 1929 година Едуин Хъбъл установява чрез наблюдения разширението на Вселената
• Гравитационното забавяне на времето е потвърдено от експеримента на Паунд-Ребка през 1959 година
• Забавянето на светлината при преминаване в близост до масивни обекти е установено от Ървин Шапиро през 1964 година
• Ефектът на Лензе-Тиринг съответства на наблюденията на „Гравити Проуб B“ от 2011 година
• Гравитационните вълни, засвидетелствани косвено при наблюдения на двойни пулсари, са пряко наблюдавани за пръв път от програмите ЛИГО и „Вирго“ през 2016 година

Бележки

Цитирани източници

• Георгиев, Владимир и др. Български етимологичен речник, Том I (А – З). София, Издателство на Българската академия на науките, 1971.
• Нарликар, Джайант. Гравитация без формул. Москва, Мир, 1985a. (на руски)
• Нарликар, Джайант. Неистовая Вселенная. Москва, Мир, 1985b. (на руски)
• Amoroso, Richard L. Gravitation and cosmology – from the Hubble radius to the Planck scale. Dordrecht, Kluwer Academic, 2002. ISBN 1-4020-0885-6. (на английски)
• Ball, Phil. Tall Tales // Nature News. June 2005. DOI:10.1038/news050613-10. (на английски)
• Gravity and Warped Spacetime // black-holes.org, 2010. Архивиран от оригинала на 2011-06-21. Посетен на 2010-10-16. (на английски)
• Bongaarts, Peter. Quantum Theory: A Mathematical Approach. Springer, 2014. ISBN 978-3-319-09561-5. (на английски)
• Born, Max. Einstein's Theory of Relativity. Dover Publications, 1962, [1924]. (на английски)
• Chandrasekhar, Subrahmanyan. Newton's Principia for the common reader. Oxford, Oxford University Press, 2003. (на английски)
• Comins, Neil F. et al. Discovering the Universe: From the Stars to the Planets. MacMillan, 2008. ISBN 978-1429230421. (на английски)
• Dyson, F. W. et al. A Determination of the Deflection of Light by the Sun's Gravitational Field, from Observations Made at the Total Eclipse of May 29, 1919 // Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 220 (571 – 581). 1920. DOI:10.1098/rsta.1920.0009. p. 291 – 333. (на английски)
• Fischbach, Ephraim et al. The search for non-Newtonian gravity. New York, Springer, 1999. ISBN 0-387-98490-9. (на английски)
• Galilei, Galileo. Dialogues Concerning Two New Sciences // oll.libertyfund.org. Liberty Fund, 2020. Посетен на 2020-03-21. (на английски)
• Goenner, H. et al. The Expanding Worlds of General Relativity // Einstein Studies (7). 1999. p. 3 – 44. (на английски)
• Grant, Edward. The Foundations of Modern Science in the Middle Ages. Cambridge, Cambridge University Press, 1996. (на английски)
• Haugen, Mark P. et al. Principles of Equivalence: Their Role in Gravitation Physics and Experiments that Test Them // Gyros 562. 2001. DOI:10.1007/3-540-40988-2_10. p. 195 – 212. (на английски)
• Black Holes: Gravity's Relentless Pull // hubblesite.org. hubblesite.org, 2016. Архивиран от оригинала на 2016-01-10. Посетен на 2016-10-07. (на английски)
• Krebs, Robert E. Scientific Development and Misconceptions Through the Ages: A Reference Guide. Greenwood Publishing Group, 1999. ISBN 978-0-313-30226-8. (на английски)
• Linton, Christopher M. From Eudoxus to Einstein—A History of Mathematical Astronomy. Cambridge, Cambridge University Press, 2004. ISBN 978-0-521-82750-8. (на английски)
• Misner, Charles W. et al. Gravitation. Freeman, 2000. ISBN 0-7167-0344-0. (на английски)
• NASA's Gravity Probe B Confirms Two Einstein Space-Time Theories // Nasa.gov. Nasa.gov, 2011. Архивиран от оригинала на 2013-05-22. Посетен на 2013-07-23. (на английски)
• Neitz, Reviel et al. The Archimedes Codex: Revealing The Secrets of the World's Greatest Palimpsest. Hachette UK, 2011-10-13. ISBN 978-1-78022-198-4. (на английски)
• Nobil, Anna M. The real value of Mercury's perihelion advance // Nature 320 (6057). March 1986. DOI:10.1038/320039a0. p. 39 – 41. (на английски)
• Pauli, Wolfgang Ernst. Part IV. General Theory of Relativity // Theory of Relativity. Courier Dover Publications, 1958. ISBN 978-0-486-64152-2. (на английски)
• Pedersen, Olaf. Early Physics and Astronomy. Cambridge, Cambridge University Press, 1993. (на английски)
• Pickover, Clifford. Archimedes to Hawking: Laws of Science and the Great Minds Behind Them. Oxford University Press, 2008. ISBN 9780199792689. (на английски)
• Pogosyan, Dmitri. Lecture 20: Black Holes – The Einstein Equivalence Principle // University of Alberta, 2011. Посетен на 2011-10-14. (на английски)
• Quinn, Terry et al. Improved Determination of G Using Two Methods // Physical Review Letters 111 (101102). 2013. DOI:https://doi.org/10.1103/PhysRevLett.111.101102. (на английски)
• G. Rosi, F. Sorrentino, L. Cacciapuoti, M. Prevedelli, G. M. Tino. Precision measurement of the Newtonian gravitational constant using cold atoms // Nature, 18 June 2014.

• Sandford, M.C.W. STEP: Satellite Test of the Equivalence Principle // Rutherford Appleton Laboratory, 2008. Архивиран от оригинала на 2011-07-16. Посетен на 2011-10-14. (на английски)
• Sen, Amartya. The Argumentative Indian. Allen Lane, 2005. ISBN 978-0-7139-9687-6. (на английски)
• Tuplin, CJ et al. Science and Mathematics in Ancient Greek Culture. Hachette UK, 2002. ISBN 978-0-19-815248-4. (на английски)
• Birth of the Universe // abyss.uoregon.edu. University of Oregon, 2016. Архивиран от оригинала на 2018-11-28. Посетен на 2016-09-24. (на английски)
• Vitruvius, Marcus Pollio. De Architectura libri decem. Cambridge, Harvard University Press, 1914. Архивиран от оригинала на 2016-10-13. (на латински)
• Weinberg, Steven. Gravitation and cosmology. John Wiley & Sons, 1972. (на английски)
• Wesson, Paul S. Five-dimensional Physics. World Scientific, 2006. ISBN 978-981-256-661-4. (на английски)

Вижте също

• Земно ускорение