Локсодрома

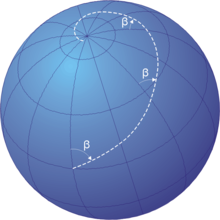
Локсодрома или Локсодромия (на гръцки: λοξóς – наклонен – и на гръцки: δρóμος – път, курс) се нарича крива, която пресича всички меридиани под еднакъв ъгъл. В морската навигация движението по локсодрома отговаря на движение по постоянен истински или магнитен курс.

История

Първите изследвания върху свойствата на локсодромата публикува португалския математик Педро Нунес в труда си „Tratado de Defensão da Carta de Marear“ през 1537 г.^[1]

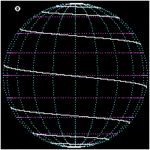
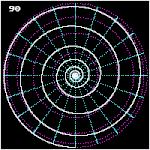
Математика

Върху сфера локсодромата е спирала. Едно от основните свойства на картите в Меркаторова проекция е изобразяването на локсодромите като прави линии.

Нека права на карта в Меркаторова проекция свързва две точки с координати $\left(\varphi _{1},\lambda _{1}\right)$ и $\left(\varphi _{2},\lambda _{2}\right)$ . Съответните правоъгълни координати $\left(x_{1},y_{1}\right)$ и $\left(x_{2},y_{2}\right)$ могат да се изчислят по ур. 1.1 и 1.2 (за сфера) или ур. 3.1 и 3.2 (за елипсоид) от трансформациите за Меркаторова проекция^[2].

Азимутът по локсодромата (или истинския курс) се изчислява по формулата:

$Az=\arctan \left[\left(x_{2}-x_{1}\right)/\left(y_{2}-y_{1}\right)\right]$

(1.1)

Истинското разстояние по локсодромата може да се изчисли по:

$s=\left(M_{2}-M_{1}\right)/\cos Az$

(1.2)

където $M_{1}$ и $M_{2}$ са съответните дължини на дъгите по меридиана от екватора за двете точки $\left(\varphi _{1},\lambda _{1}\right)$ и $\left(\varphi _{2},\lambda _{2}\right)$ . Те могат да се изчислят по генерализираната формула за $M$ :

При известни

a-

голяма полуос на референтния елипсоид

e-

ексцентрицитет на референтния елипсоид

$M=a\left(1-e^{2}\right)\int _{0}^{\varphi }\left[{\frac {1}{\left(1-e^{2}\sin ^{2}\varphi \right)^{3/2}}}\right]\,d\varphi$

(1.3)

или като числов ред:

${\begin{aligned}M=a[&\left(1-e^{2}/4-3e^{4}/64-5e^{6}/256-...\right)\varphi -\\&\left(3e^{2}/8+3e^{4}/32+45e^{6}/1024+...\right)\sin 2\varphi +\\&\left(15e^{4}/256+45e^{6}/1024+...\right)\sin 4\varphi -\\&\left(35e^{6}/3072+...\right)\sin 6\varphi +\\&...]\end{aligned}}$