Кубоид

Кубоид се нарича геометрично тяло, което е шестостен (хексаедър) с четириъгълни лица, което означава, че има 6 стени, 8 върха и 12 ръба. Етимологично „кубоид“ означава „като куб“, в смисъл на изпъкнало тяло, което може да се трансформира в куб (чрез регулиране на дължините на ръбовете и ъглите между съседните му страни). Кубоидът е изпъкнал многостен, чийто многостенен граф е същият като този на куб.^[1] Думата „кубоид“ също се използва, за да се опише по-общ клас от изпъкнали политопи в три или повече измерения, получени чрез залепване заедно на политопи, комбинаторно еквивалентни на хиперкубове.^[2]

Общите кубоиди имат много различни видове. Когато всички ръбове на правоъгълния кубоид са еднакви по дължина, това води до куб с шест квадратни стени, от които съседните се срещат под прав ъгъл.^[1]^[3] Правоъгълният кубоид, наричан още правоъгълен паралелепипед, има всички прави ъгли и равни срещуположни правоъгълни стени. Паралелепипедът е кубоид с шест успоредника (3 двойки успоредни стени). Ромбоедърът е кубоид с 6 стени с формата на ромб. Квадратният фрустум (геометрично тяло между два успоредни квадрата) е фрустум с квадратни основи, но страничните му стени са четириъгълници; квадратният фрустум се образува чрез отрязване на върха на квадратна пирамида и се нарича „правилна пресечена четириъгълна пирамида“ или „квадратна пресечена пирамида“. В опит да класифицира кубоидите по техните симетрии Робъртсън (1983) открива, че има най-малко 22 различни случая, „от които само около половината са познати във формите на ежедневни предмети“.^[4]

Някои забележителни кубоиди
(четириъгълeн изпъкнал шестостен • 8 върха и 12 ръба)
Име	Стени	Група на симетрия
Куб	6 еднакви квадрата	O_h, [4,3], (*432) ред 48
Правилен ромбоедър (Триъгълен трапецоедър)	6 еднакви ромба	D_3d, [2⁺,6], (2*3) ред 12
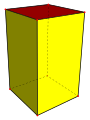Правилен паралелепипед (Квадратен паралелепипед)	2 еднакви квадрата, 4 еднакви правоъгълника	D _4h, ?, ? ред 16
Правоъгълен паралелепипед (Права правоъгълна призма)	3 двойки от еднакви правоъгълници	D _2h, [2,2], (*222) ред 8
Ромбичен кубоид	2 еднакви ромба, 4 еднакви квадрата
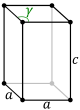Права ромбична призма (прав ромбичен паралелепипед)	2 еднакви ромба, 4 еднакви правоъгълника
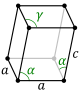Наклонена ромбична призма (ромбичен паралелепипед)	2 еднакви ромба, 4 еднакви успоредника	C_2h, ред 4
Прав паралелепипед	2 еднакви успоредника, 4 еднакви правоъгълника	C_2h, ред 4
Ромбична призма	6 ромба	C_2h, [2] ред 4
Права пресечена квадратна пирамида (Прав квадратен фрустум)	2 различни квадрата, 4 еднакви равнобедрени трапеца	C_4v, [4], (*44) ред 8
Усукан триъгълен трапецоедър	6 еднакви четириъгълници	D₃, [2,3]⁺, (223) ред 6
Права равнобедрена трапецовидна призма	1 двойка равнобедрени трапеци; 1, 2 или 3 (еднакви) квадрат(а)	?, ?, ? ред 4
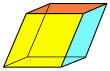Ромбоедър	3 двойки от еднакви ромбове	C_i , [2⁺,2⁺], (×) ред 2
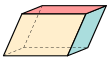Паралелепипед	3 двойки от еднакви успоредници	C_i , [2⁺,2⁺], (×) ред 2

Съществуват шестостени (хексаедри) с четириъгълно лице, които не са изпъкнали.

Вижте също

Източници

↑ ^а ^б Robertson, Stewart A. – Polytopes and Symmetry. Cambridge University Press, 1984, p. 75. ISBN 9780521277396.
↑ Grünbaum, Branko – Convex Polytopes. Graduate Texts in Mathematics. Vol. 221 (2^nd ed.). New York, Springer-Verlag, 2003, p. 59. doi:10.1007/978-1-4613-0019-9. ISBN 978-0-387-00424-2. MR 1976856.
↑ Dupuis, Nathan F. – Elements of Synthetic Solid Geometry. Macmillan, 1893, p. 53. Retrieved December 1, 2018.
↑ Robertson, S. A. – Polyhedra and symmetry. Mathematical journal „The Mathematical Intelligencer“, 1983, 5 (4): p. 57–60. doi:10.1007/BF03026511. MR 0746897.

[PS-1] а ^б Robertson, Stewart A. – Polytopes and Symmetry. Cambridge University Press, 1984, p. 75. ISBN 9780521277396.

[2] Grünbaum, Branko – Convex Polytopes. Graduate Texts in Mathematics. Vol. 221 (2^nd ed.). New York, Springer-Verlag, 2003, p. 59. doi:10.1007/978-1-4613-0019-9. ISBN 978-0-387-00424-2. MR 1976856.

[3] Dupuis, Nathan F. – Elements of Synthetic Solid Geometry. Macmillan, 1893, p. 53. Retrieved December 1, 2018.

[4] Robertson, S. A. – Polyhedra and symmetry. Mathematical journal „The Mathematical Intelligencer“, 1983, 5 (4): p. 57–60. doi:10.1007/BF03026511. MR 0746897.

[1]

[2]

[3]

[4]