Квадратно уравнение

Квадратно уравнение в математиката се нарича уравнение от втора степен от вида

ax^{2}+bx+c=0

,

където $x$ е неизвестното, а коефициентите $a,b$ и $c$ са реални или комплексни числа и $a\neq 0$ .
Ако $a\neq 0,c\neq 0$ и $b=0$ или $a\neq 0,b\neq 0$ и $c=0$ , уравнението е непълно квадратно,
а при $a=0$ и $b\neq 0$ то става линейно.

Лявата страна на квадратното уравнение

ax^{2}+bx+c

е многочлен (полином) от втора степен и се нарича квадратен тричлен.

Корен на квадратното уравнение $ax^{2}+bx+c=0$ е всяка стойност на неизвестното $x$ , за която се изпълнява равенството. Тази стойност се нарича още корен на квадратния тричлен $ax^{2}+bx+c$ .

Елементите на квадратното уравнение имат свои имена:^[1]

$a$ се нарича първи или водещ коефициент,
$b$ се нарича втори, среден коефициент или коефициент на $x$ ,
$c$ се нарича свободен член.

Нормирано уравнение или приведено в нормиран вид е квадратно уравнение, в което водещият коефициент е равен на единица $a=1$ .^[1] Привеждането се извършва чрез разделяне на цялото уравнение на водещия коефициент $a$ :

x^{2}+px+q=0,\quad p={\dfrac {b}{a}},\quad q={\dfrac {c}{a}}

.

Решаване на квадратни уравнения

Решаването на квадратното уравнение, както на всяко уравнение, се заключава в изчисляване на неговите корени. Това може да стане по различни методи и начини за различни случаи.

I метод. Обща формула за изчисляване на корени с дискриминанта

Пълното квадратно уравнение се решава по следния начин:

ax^{2}+bx+c=0

ax^{2}+bx=-c

Умножава се всяка част на $4a$ и се прибавя $b^{2}$ :

4a^{2}x^{2}+4abx+b^{2}=-4ac+b^{2}

(2ax+b)^{2}=b^{2}-4ac

.

Дискриминанта на квадратното уравнение $ax^{2}+bx+c=0$ се нарича величината ${\mathcal {D}}=b^{2}-4ac$ .

За случая ${\mathcal {D}}>0$

2ax+b=\pm {\sqrt {b^{2}-4ac}}

2ax=-b\pm {\sqrt {b^{2}-4ac}}

x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}

(1)

x_{1,2}={\frac {-b\pm {\sqrt {\mathcal {D}}}}{2a}}.

Формулата за случая ${\mathcal {D}}=0$ е частен случай на формула (1):

x={\frac {-b\pm {\sqrt {\mathcal {D}}}}{2a}}={\frac {-b\pm {\sqrt {0}}}{2a}}=-{\frac {b}{2a}}.

За случая ${\mathcal {D}}<0$ квадратният корен от отрицателно число не е реално число. Уравнението няма реални корени и решението се получава от формула (1) във вид на два комплексни корена:

x_{1,2}={\frac {-b\pm j{\sqrt {\mathcal {D}}}}{2a}}

. (2)

Условие	${\mathcal {D}}>0$	${\mathcal {D}}=0$	${\mathcal {D}}<0$
Брой корени	Два различни реални корена	Един двоен корен (два равни корена)	Няма реални корени – 2 комплексни корена
Формула	$x_{1,2}={\frac {-b\pm {\sqrt {\mathcal {D}}}}{2a}}$ (1)	$x=-{\frac {b}{2a}}$	$x_{1,2}={\frac {-b\pm j{\sqrt {\|{\mathcal {D}}\|}}}{2a}}$ (2)

Следствия:

тричленът $ax^{2}+bx+c$ е идеален квадрат на сума или разлика тогава и само тогава, когато ${\mathcal {D}}=0$ ;
Дискриминантата може да се намери с формулата: ${\mathcal {D}}=a^{2}\left(x_{+}-x_{-}\right)^{2}$ ;
$x_{\pm }={\frac {2c}{-b\mp {\sqrt {\mathcal {D}}}}}$ .

Този метод е универсален, но не единствен.

II метод. Съкратена формула при четен коефициент b

За уравнения от вида

ax^{2}+2kx+c=0

,

където $k={\frac {b}{2}}$ , тоест за четно $b$ , вместо формула (1) за намиране на корените е възможно да се използват по-прости изрази.^[1]

Забележка: Формулите по-долу за ненормирано и нормирано квадратно уравнение могат да бъдат получени след заместване на израза $b=2k$ в стандартните формули чрез прости преобразования. По-удобно е да се изчисли стойността на четвърт дискриминанта ${\frac {D}{4}}$ , при което всички необходими свойства са запазени.

Дискриминанта		Корени
ненормирано	нормирано	D > 0	ненормирано	нормирано
${\frac {D}{4}}=k^{2}-ac$ ;	${\frac {D}{4}}=k^{2}-c$ .	D > 0	$x_{1,2}={\frac {-k\pm {\sqrt {k^{2}-ac}}}{a}};$	$x_{1,2}=-k\pm {\sqrt {k^{2}-c}}$ .
${\frac {D}{4}}=k^{2}-ac$ ;	${\frac {D}{4}}=k^{2}-c$ .	D = 0	$x={\frac {-k}{a}}$	$x=-k$

III метод. Решаване на непълни квадратни уравнения

Използва се специален подход за решаване на „непълни“ квадратни уравнения. Разглеждат се три възможни ситуации.

b = 0; c = 0

b = 0; c ≠ 0

b ≠ 0; c = 0

{\begin{alignedat}{2}ax^{2}&=0,\\x^{2}&=0,\\x&=0.\end{alignedat}}

(Процесът на преобразуване е специално показан в детайли; на практика може веднага да се премине към последното равенство.)

{\begin{aligned}ax^{2}+c&=0,\\ax^{2}&=-c,\\x^{2}&=-{\dfrac {c}{a}},\\x_{1,2}&=\pm {\sqrt {-{\dfrac {c}{a}}}}.\end{aligned}}

Ако

-{\dfrac {c}{a}}>0

, тогава уравнението има два реални корена (различни по знак) и ако

-{\dfrac {c}{a}}<0

, тогава уравнението няма реални корени.

{\begin{aligned}ax^{2}+bx&=0,\\x(ax+b)&=0,\end{aligned}}

$x=0$ или $ax+b=0,$ $x_{1}=0,\quad x_{2}=-{\dfrac {b}{a}}.$

Такова уравнение „непременно има два реални корена“, като единият от тях винаги е равен на нула.

IV метод. Използване на частни съотношения на коефициенти

Има специални случаи на квадратни уравнения, в които коефициентите са във връзка един с друг, което ги прави много по-лесни за решаване.

Корени на квадратно уравнение, в което сборът от водещия коефициент и свободния член е равен на втория коефициент

Ако в квадратно уравнение $ax^{2}+bx+c=0$ сборът от първия коефициент и свободния член е равен на втория коефициент $a+c=b$ , тогава корените на уравнението са $-1$ и числото, противоположно на отношението на свободния член към водещия коефициент $-{\frac {c}{a}}$ .

От това следва, че преди решаването на всяко квадратно уравнение е препоръчително да се провери възможността за прилагане на тази теорема към него: сравнява се сумата от водещия коефициент и свободния член с втория коефициент.

Корени на квадратно уравнение, чиято сума от всички коефициенти е нула

Ако в едно квадратно уравнение сумата от всички коефициенти е равна на нула $a+b+c=0$ , тогава неговите корени са $1$ и съотношението на свободния член към водещия коефициент ${\frac {c}{a}}$ .

От това следва, че преди да се реши уравнение с помощта на стандартни методи, е препоръчително да се провери приложимостта на тази теорема към него, а именно дали сумата от всичките му коефициенти не е равна на нула.

Решения на квадратно уравнение с частни съотношения на коефициентите
Съотношение на коефициентите	$x_{1}$	$x_{2}$
$a+c=-b$ $(a+b+c=0)$	$1$	${\frac {c}{a}}$
$a+c=b$	$-1$	$-{\frac {c}{a}}$

V метод. Разлагане на квадратния тричлен на линейни множители

Ако квадратният тричлен : $f(x)=ax^{2}+bx+c$ има неотрицателна дискриминанта, той се разлага на линейни множители по следния начин:

f(x)=a(x-x_{1})(x-x_{2}),

където $x_{1},x_{2}$ са корените на уравнението $f(x)=0$ .

Ако дискриминантата на квадратния тричлен е отрицателна, той не може да се разложи на линейни множители с реални коефициенти. В този случай казваме, че квадратният тричлен е неразложим.

Членът $x-r$ е множител на квадратния тричлен

ax^{2}+bx+c\,\!

тогава и само тогава, когато $r$ е корен на квадратното уравнение

ax^{2}+bx+c=0.\,\!

Това следва от формулата за разлагане на квадратно уравнение на множители

ax^{2}+bx+c=a\left(x-{\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\right)\left(x-{\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}\right),\,\!

или при $a=1$

x^{2}+bx+c=\left(x-{\frac {-b+{\sqrt {b^{2}-4c}}}{2}}\right)\left(x-{\frac {-b-{\sqrt {b^{2}-4c}}}{2}}\right).\,\!

В специалния случай, когато квадратното уравнение има един двоен корен, т.е. дискриминантата е нула, квадратният тричлен може да се разложи на множителите:

ax^{2}+bx+c=a\left(x+{\frac {b}{2a}}\right)^{2}.\,\!

Така чрез разлагане на квадратния тричлен на линейни множители решаването на квадратното уравнение се свежда до решаването на линейни уравнения.

VI метод. Допълване до точен квадрат на нормирано уравнение

Уравнението

x^{2}+px+q=0\quad

се решава чрез допълване до точен квадрат. Това е често прилаган в практиката метод, както при пълното квадратно уравнение (I метод):

x^{2}+px+{\frac {p^{2}}{4}}-{\frac {p^{2}}{4}}+q=0\quad

x^{2}+px+{\frac {p^{2}}{4}}={\frac {p^{2}}{4}}-q\quad

\left(x+{\frac {p}{2}}\right)^{2}={\frac {p^{2}}{4}}-q\quad

x+{\frac {p}{2}}=\pm {\sqrt {{\frac {p^{2}}{4}}-q}}\quad

x=-{\frac {p}{2}}\pm {\sqrt {{\frac {p^{2}}{4}}-q}}\quad

Ако в реалния случай тук се получи под корена отрицателно число, последните две стъпки естествено не са допустими. В този случай на третия ред се вижда, че не може да има реално решение, защото дясната страна е отрицателна, а лявата като квадрат не е отрицателна.

Методът може да се разглежда като частен случай на разлагане на квадратния тричлен на еднакви линейни множители.

VII метод. Формули на Виет

Полезни връзки между корените и коефициентите на квадратното уравнение са установени от френския математик Франсоа Виет през XVII в. и поради това носят неговото име.

Права теорема на Виет: Ако $x_{1}$ и $x_{2}$ са корените на квадратното уравнение

ax^{2}+bx+c=0

, то

x_{1}+x_{2}=-{\frac {b}{a}}

,

x_{1}x_{2}={\frac {c}{a}}.

Обратна теорема на Виет: Ако числата $x_{1}$ и $x_{2}$ са такива, че $x_{1}+x_{2}=p$ и $x_{1}.x_{2}=q$ , то тези числа са корени на уравнението $x^{2}-px+q=0$ .

VIII метод. Преобразуване със заместване

По своята същност този метод е просто модификация на теоремата на Виет.

Методът „Преобразуване със заместване“ е привеждане на уравнение, което не може да се преобразува така, че всичките му коефициенти да останат цели, към нормирано квадратно уравнение с цели коефициенти чрез смяна на променливата:

1) Умножават се двете части на уравнението по водещия коефициент $a$ :

ax^{2}+bx+c=0\quad \mid \;\cdot a,

(ax)^{2}+b(ax)+ac=0;

2) Замества се $ax\colon =y$

y^{2}+by+ac=0.

Решава се полученото уравнение спрямо $y$ по описания метод за нормирано уравнение и после се намира $x={\frac {y}{a}}$ .

Графично решение на квадратно уравнение

За квадратната функция
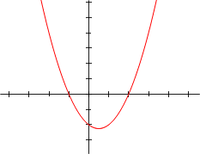
$f(x)=x^{2}-x-2=(x+1)(x-2)$ на реалната променлива $x$ , абсцисите на точките, в които графиката пресича оста $x$ , а именно $x=-1$ и $x=2$ , са корени на квадратното уравнение $x^{2}-x-2=0$ .

Корените на квадратното уравнение

ax^{2}+bx+c=0,\,

са и нули на квадратната функция

f(x)=ax^{2}+bx+c,\,

тъй като те са стойности на x, за които

f(x)=0.\,

Ако $a,b$ и $c$ са реални числа и дефиниционната област на $f$ е множеството на реалните числа, тогава нулите на $f$ са абсцисите на точките, в които графиката на функцията $f$ пресича оста $x$ . От горното следва, че ако дискриминантата е положителна, графиката пресича оста $x$ в две точки; ако тя е нула, графиката се допира до оста $x$ в една точка и ако е отрицателна, графиката не пресича оста $x$ .

Уравнения, които се свеждат към квадратни

Алгебрични

Уравнения от висока степен като

2x^{6}+3x^{3}+5=0

могат да се сведат до квадратни уравнения

2u^{2}+3u+5=0

,

където

u=x^{3}

.

Забележително е, че най-високата степен е равна на удвоената степен на средния член. Полученото квадратно уравнение може да се реши директно или с проста субституция, като се използват методите за решаване на квадратни уравнения като разлагане на множители, допълване до точен квадрат и др.

Най-общо, ако полиномът е квадратен тричлен относно някоя променлива $u$ , където