Средно квадратично
В математиката средно квадратична (СК, ск) или ефективна стойност (на английски: Root mean square, RMS или rms), е статистическа мярка за големината на променлива величина, която е частен случай на средностепенната стойност при степенен показател . Понятието е особено полезно, когато величините са положителни и отрицателни, например при синусоидално разпределение на стойностите. Терминът се използва в различни области на науката. В частност, чрез него се определя основното понятие в теорията на вероятностите и математическата статистика – дисперсията (квадратният корен от която се нарича средноквадратично отклонение). Тясно свързан с това понятие е методът на най-малките квадрати, който има общонаучно значение. В частност, терминът широко се използва в електротехниката; напр. при дефиниране на ефективната стойност на ток, напрежение и мощност.[1][2]
Определение
[редактиране | редактиране на кода]Средноквадратична стойност на набор от величини (или непрекъсната функция) е квадратен корен от средно аритметичното на квадратите на оригиналните стойности (или квадрата на функцията, която определя непрекъснатата форма).
В случай на набор от стойности , средноквадратичната стойност се определя чрез израза:
Може да бъде записана също и във вида:
Претеглено средноквадратично се изчислява по формулата:
Съответната формула за непрекъсната функция (или форма) , определена в интервала , е:
а средноквадратичната стойност за функция в целия обхват на време е:
Когато функцията е периодична, средноквадратичната стойност за произволен обхват от време е равна на средноквадратичната стойност само за един пълен период на функцията. [1] Средноквадратичната стойност на непрекъсната функция или сигнал може да бъде приближена чрез изчисляване на средноквадратичната стойност на серии от дискретни стойности на функцията, взети през еднакъв интервал от време.
Във функционалния анализ и теорията на измерването средната квадратична конвергенция се определя като конвергенция на редица в смисъла на нормата за двумерно пространство .
За означаване на СК се използват още символите , и (нотация, често използвана във физиката, където ⟨ ⟩ означава средно аритметично).
Свойства
[редактиране | редактиране на кода]- Средноквадратичното на набор от неотрицателни числа лежи между минималното и максималното число на набора.
- Средноквадратичната стойност е частен случай на средностепенната и следователно се подчинява на неравенството на средните стойности. По-специално, за всякакви числа средноквадратичното не е по-малко от средноаритметичното:
Например: e по-малко от
Употреба
[редактиране | редактиране на кода]Стандартното отклонение в съвкупността е средноквадратичната стойност на разликите от средната стойност.
Средноквадратичната стойност трябва да се използва, когато се търси осредняване на количество, което влияе на квадрата в дадено явление. Такъв е случаят например със скоростта на частиците в среда. Всяка частица се движи със скорост и произвежда кинетична енергия, равна на 1⁄2. Средата отделя кинетична енергия
Можем да опитаме да оценим скоростта , която, приложена към същия брой частици, ще даде същата кинетична енергия. Тази скорост е средната квадратична стойност на всички скорости. [3]
Във физиката СК скорост се определя като корен квадратен от средната квадратна скорост на молекулите в газ. Средната квадратична скорост на идеален газ се изчислява с помощта на следното уравнение:
където представлява идеалната газова константа (в този случай 8,314 J/(mol*K)), е температурата на газа в келвини, а е моларната маса на газа в килограми.
В общи вълнови форми
[редактиране | редактиране на кода]Ако формата на вълната е периодична, връзките между амплитудите (пик или от пик до пик) и СК са фиксирани и известни, както са за всяка непрекъсната периодична вълна.
За нулева средна синусоида връзката между СК и амплитудата от пик до пик е

а между СК и амплитудата пик :
За триъгълна или трионообразна вълна – съответно:
За други форми на вълната, връзките са различни. В общия случай формата на вълната е произволна и може да не е периодична или непрекъсната.
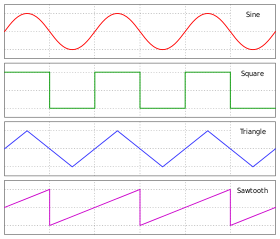

| Вълнови форми | Формула | СК |
|---|---|---|
| Синусоидална вълна | ||
| Квадратна вълна без пауза | ||
| Квадратна вълна с пауза | ||
| Трионообразна вълна | ||
| Означения: – времe – чeстота – aмплитуда (пикова стойност) – остатък от етажното деление | ||
В електротехниката
[редактиране | редактиране на кода]Ефективните стойности на променливи ток , напрежение и мощност във времето с период са равни на съответните им постоянни стойности , , , определящи същата енергия във верига със съпротивление :
Ефективната стойност на променлив ток във времето с период е равна на интензитета на постоянния ток, излъчващ същата енергия като , преминавайки през съпротивление за период :
Тогава ефективната стойност се изразява като квадратен корен от средно аритметичното на квадрата на тока за период :
Ефективната стойност на променливо напрежение е стойността на постоянното напрежение, което излъчва същата енергия като променливото напрежение , ако се приложи на изводите на същото съпротивление :
От тук за ефективната стойност на напрежението се получава:
Ефективната стойност на променлива мощност за период е стойността на постоянната мощност, която съответства на същата енергия, излъчена от същото съпротивление :
Математически се изразява чрез:
Нарича се още средна електрическа мощност . Ако токът и напрежението са променяща се функция във времето, във формулите за и трябва да се замести видът на тази функция. Ако функцията е периодична (като променливотоковото захранване за масова употреба), средната мощност, разсейвана във времето, е средна стойност на мощността във всеки момент във формата на вълната или, еквивалентно, средният квадрат на тока или напрежението. Тогава, при постоянно съпротивление на консуматора за средната мощност, изразена чрез тока се получава
или изразена чрез напрежението
Чрез умножаване и коренуване на последните две уравнения средната мощност се изразява чрез ефективните стойности на напрежението и тока:
Получените резултати се отнасят за случая, когато напрежението и токът са пропорционални (т.е. товарът е чисто резистивен). Реактивните товари не само разсейват енергия, но и я съхраняват, което води до загуби.
В обичайния случай, както е приблизително в мрежовото захранване, променливият ток е синусоидален: , където e пиковата амплитуда на тока, е времето и е ъгловата честота. Тогава:
Тъй като е положителна константа, след тригонометрично преобразуване и интегриране се получава:
но тъй като интервалът е цял брой пълни цикли (по дефиниция на СК), и остава:
Подобен анализ води до аналогичното уравнение за синусоидално напрежение:
с пикова амплитуда . Струва си да се повтори, че тези две .
Получените решения за синусоидална вълна са полезни при изчисления на мощността. Ефективната (СК) стойност на променливото напрежение е 230 V в Европа и 120 V в САЩ. Амплитудните пикови стойности могат да бъдат изчислени от СК стойности по горната формула, което означава , като се приеме, че източникът е чиста синусоида. Така за Европа пиковата стойност на мрежовото напрежение е волта, а напрежението от пик до пик е два пъти повече – волта. В САЩ пиковата амплитуда е около 170 волта, а от пик до пик е около 340 волта.
Аналогично може да се изчисли и пиковата мощност. Тя няма особено физическо значение и се използва най-често в звуковата техника.
| Сигнал | Форма на вълната | I | U | P |
|---|---|---|---|---|
| Синусоидален | 
|
|||
| Триъгълен | 
|
|||
| Квадратен симетричен (без пауза) |
|
Коефициент на полезно действие на усилвателя
[редактиране | редактиране на кода]Коефициент на полезно действие на електронния усилвател е съотношението на средната изходна мощност към средната входна мощност . Ако изходът е резистивен, средната изходна мощност може да се намери по описания начин чрез СК стойности на изходния ток и напрежение на сигналите. Въпреки това, средната стойност на тока трябва да се използва за изчисляване на входната мощност. Тоест, мощността, доставена от усилвателя чрез постоянното напрежение е
където е работният ток на усилвателя. Ясно е, че тъй като е константа, средното време на зависи от средната времева стойност на , а не от неговата СК стойност. Това е
Средноквадратична непрекъснатост на пространствен процес
[редактиране | редактиране на кода]Определение — Процес от втори ред X върху пространствено множество S ⊂ ℝd е непрекъснат средноквадратично, ако за всяка конвергентна последователност sn → s от S, E[X(sn) − X(s)]2 → 0.
Характеризиране — Центриран процес е непрекъснат средноквадратично навсякъде, ако неговата ковариация е непрекъсната по диагонала на неговото пространствено множество.
Непрекъснатостта по диагонала означава, че ковариацията C(s, s) е непрекъсната за всички s в пространственото множество.
Теорема — Ако присъщ Гаусовски процес с вариограма γ проверява γ(h) ≤ |log∥h∥|−(1+ε) в близост до началото, тогава той почти сигурно е непрекъснат.
Такъв е случаят с всички стандартни модели на вариограми, с изключение на модела с ефект на самородно късче.
Теорема — Един присъщ процес е средноквадратично непрекъснат, ако неговата вариограма е непрекъсната в началото.
Стационарен процес от втори ред е средноквадратично непрекъснат, ако неговата ковариация е непрекъсната в началото.[4][3]
Средноквадратична диференцируемост на едномерен процес
[редактиране | редактиране на кода]Източници
[редактиране | редактиране на кода]- ↑ а б Речник на научните термини – Е. Б. Уваров, А. Айзакс. Издателство „Петър Берон“, 1992.
- ↑ Квадратичное среднее. Большой Энциклопедический словарь. 2000. (на руски)
- ↑ а б Moyennes (II) : la moyenne quadratique Архив на оригинала от 2022-12-08 в Wayback Machine. – Ecrit par Kloeckner, BenoîtLe, 15 août 2009.
- ↑ Въведение в стохастичните процеси – Г. Бошнаков, Стилян Стоев, Д. Въндев, 1999–2008.
| Тази страница частично или изцяло представлява превод на страницата Root mean square и страницата Valeur efficace в Уикипедия на английски и френски език. Оригиналните текстове, както и този превод, са защитени от Лиценза „Криейтив Комънс – Признание – Споделяне на споделеното“, а за творби, създадени преди юни 2009 година – от Лиценза за свободна документация на ГНУ. Прегледайте историята на редакциите на оригиналните страници тук и тук, за да видите списъка на техните съавтори.
ВАЖНО: Този шаблон се отнася единствено до авторските права върху съдържанието на статията. Добавянето му не отменя изискването да се посочват конкретни източници на твърденията, които да бъдат благонадеждни. |
| Тази страница частично или изцяло представлява превод на страницата „Среднее квадратическое“ в Уикипедия на руски. Оригиналният текст, както и този превод, са защитени от Лиценза „Криейтив Комънс – Признание – Споделяне на споделеното“, а за съдържание, създадено преди юни 2009 година – от Лиценза за свободна документация на ГНУ. Прегледайте историята на редакциите на оригиналната страница, както и на преводната страница, за да видите списъка на съавторите.
ВАЖНО: Този шаблон се отнася единствено до авторските права върху съдържанието на статията. Добавянето му не отменя изискването да се посочват конкретни източници на твърденията, които да бъдат благонадеждни. |









![{\displaystyle f_{\mathrm {ck} }={\sqrt {{1 \over {T_{2}-T_{1}}}{\int _{T_{1}}^{T_{2}}{[f(t)]}^{2}\,dt}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f5c783e3145f0c2b1d7057f955c50f3a5d92376)
![{\displaystyle f_{\mathrm {CK} }=\lim _{T\rightarrow \infty }{\sqrt {{1 \over {2T}}{\int _{-T}^{T}{[f(t)]}^{2}\,dt}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdffab8c1d9d29e019402c8c439565b364dfd4da)































































![{\displaystyle =I_{\mathrm {m} }{\sqrt {{1 \over {T_{2}-T_{1}}}\left[{{t \over 2}-{\sin(2\omega t) \over 4\omega }}\right]_{T_{1}}^{T_{2}}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9025353364116d8730cb7e1786adc74e6b286069)


![{\displaystyle I_{\mathrm {CK} }=I_{\mathrm {m} }{\sqrt {{1 \over {T_{2}-T_{1}}}\left[{t \over 2}\right]_{T_{1}}^{T_{2}}}}=I_{\mathrm {m} }{\sqrt {{1 \over {T_{2}-T_{1}}}{{T_{2}-T_{1}} \over 2}}}={I_{\mathrm {m} } \over {\sqrt {2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5d22e0a918e211e757ec01f19358c263deb80b8)





















