Синус

Вижте пояснителната страница за други значения на Синус.

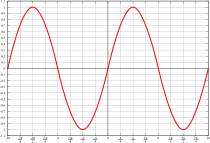
Синус е една от тригонометричните функции. Бележи се със sin x. Графиката на функцията се нарича синусоида.

Дефиниция

За остър ъгъл в правоъгълен триъгълник синусът се дефинира като съотношението на срещулежащия катет към хипотенузата. За обобщен ъгъл с радианна мярка x, чийто връх е в координатното начало, а първото рамо е по абсцисната ос, sin x е ординатата на точката, в която второто рамо на ъгъла пресича единичната окръжност.

Формули и свойства

Синус на ъгъл Θ се нарича отношението на ординатата на точка A към дължината на отсечката OA. Означава се със sin Θ = AC / OA. Тъй като дължината на отсечката OA = 1, то sin Θ = AC.

Някои от свойствата на функцията синус са:

Нечетна функция – понеже sin(-x) = -sin x
Периодична функция с период 2π, понеже sin x = sin(x+2kπ)
Ограничена функция – и отгоре от 1, и отдолу от -1.
За функцията синус е изпълнено основното тригонометрично тъждество sin²x + cos²x = 1.
Синус от много малък ъгъл е приблизително равен на самия ъгъл

Синус на удвоен ъгъл

sin 2x = 2sin x.cos x.

Синус на сбор и разлика на два ъгъла

sin(x+y) = sin x.cos y + sin y.cos x.

sin(x-y) = sin x.cos y - sin y.cos x.

История

Функцията синус се среща още в индийските сидханти – анонимни трудове по астрономия от IV-V в. и в „Ариабхатим“ – съчинение по астрономия и математика на Ариабхата (499 г.). Синусоидата се е наричала „ардхаджива“, което идва от „ардха“ – „половина“ и „джива“ – „тетива на лък“, „хорда“. В течение на времето терминът е бил съкратен на „джива“, а в арабската литература навлиза като „джиба“. През IX в. лишената от ежедневен смисъл заемка е заменена с реалната арабска дума „джайб“, която значи „пазва“, „деколте“, „изпъкналост“.

При преводите от арабски на латински преводачите Робърт Честърски (1145) и Герардо Кремонски (1175) употребяват буквалния превод на „джайб“ – sinus. В ръкописи от XII в. се среща дори латинската транскрипция „geib“. До XV в. се среща и терминът на Птолемей – „хорда на удвоената дъга“.

За означаване на синуса на ъгъл са използвани различни съкращения – s, si, sin, S и др. Авторитетът на Леонард Ойлер спомага да се наложат означенията sin, cos, tg в тригонометрията. Той предлага да се дефинират тригонометричните функции като отношение на съответната отсечка към радиуса на окръжността.

Първите таблици на синусите в Европа са съставени през XV в. от Пойрбах, а по-късно и от неговия ученик Йохан Региомонтан. Николай Коперник предлага подобрения през 1551 г., а през 1610 г. Бартоломеус Питискус съставя 16-значни таблици през всеки 10 ъглови секунди (1/3600 част от градуса).

Източници

„Лексикон Математика“, Георги Симитчиев, Георги Чобанов, Иван Чобанов, „Абагар Холдинг“, София, 1995
„Математически термини“, Н. В. Александрова, ДИ „Наука и изкуство“, София, 1989
„Математически енциклопедичен речник“, Валтер Гелерт, Херберт Кестнер, Зигфрид Нойбер, ДИ „Наука и изкуство“, София, 1983

Вижте също

Външни препратки