Размерност

Тази статия е за математическата концепция. За музикалното понятие вижте Размерност (музика).

---

Размерност или измерение е понятие, с което в математиката се уточнява и формализира обичайното разбиране, че в пространството има три посоки (напред, встрани, нагоре) и съответно предметите могат да имат дължина, ширина и височина, т.е да са тримерни (или три-измерни). На плоскостите се приписва размерност 2, а на линиите – 1. Това съответства на факта, че при дадена отправна система за еднозначното определяне на точка от пространството са необходими три числа, а при повърхнина или линия съответно две или едно. Различни дефиниции възпроизвеждат тези положения, но отвъд тях, с оглед на нуждите, за които се формулират, между тях има различия. Така например на фракталните обекти може да бъде приписвана нецяла размерност, а във физиката размерността да бъде променлива. Най-общо размерността се свързва с число, което изразява какво количество информация е нужно за описанието на съответния обект.

В математиката

От ляво надясно: квадрат, куб и тесеракт. Двуизмерният квадрат е ограничен с едноизмерни линии, триизмерният куб е ограничен с двуизмерни равнини, а четириизмерният тесеракт е ограничен от триизмерни обеми. За изобразяване върху двуизмерна повърхност (например екран на монитор) кубът и тесерактът са представени чрез подходящи проекции

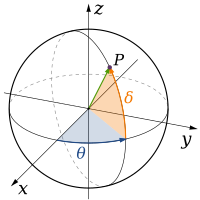
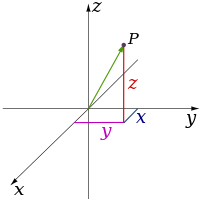
В математиката, измерението на пространството най-общо се определя като минималният брой координати, необходим за еднозначно посочване на всяка точка в него. Например: в равнината, която е двуизмерна, всяка точка от една окръжност може да бъде определена с две декартови координати. Със задаването на описанието „окръжност“, на комбинациите от координати се налага ограничение, така че когато е известна едната от тях, може да бъде посочена другата и в този смисъл окръжността, като линия е едномерна. В полярна координатна система, при зададен радиус единствената координата е полярният ъгъл и така окръжността се приема като едноизмерна.

Във физиката

Различните посоки в триизмерно пространство, X-напред/назад Y-наляво/надясно Z-нагоре/надолу

Пространство

Класическата физика използва три измерения за описване на взаимното разположение на предметите: от определена точка в пространството можем да се движим нагоре/надолу, надясно/наляво и напред/назад. Движението във всички други посоки може да се представи като комбинация от тези три. В най-проста форма това звучи така: линията (правата) описва едно измерение, равнината – две, а кубът – три измерения. (виж Пространство и Декартова координатна система.)

Брой измерения	Примерни координатни системи
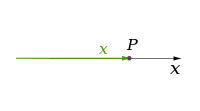
1	Числова ос Ъгъл
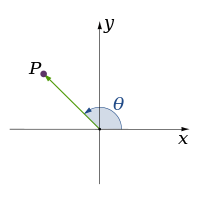
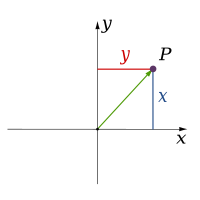
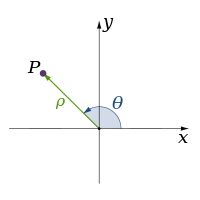
2	Декартова (2-измерна) Полярна Географска ширина и дължина
3	Декартова (3-измерна) Цилиндрична Сферична

Време

В класическите представи на геометрията време не се използва, но още в края на 18 век Лагранж отбелязва, че механиката представлява „четиримерна геометрия“. Математическият формализъм наистина позволява в почти всички случаи времето да се третира също както пространствените координати. Физически обаче то остава различно – посоката му е единствена и не може да се движим свободно във времето, а само от настояще към бъдеще.

В теорията на относителността се въвежда терминът пространство-време, който комбинира пространството и времето в единен пространствено-временен континуум. Основание за това е фактът, че в природата съществува горна граница на скоростите.

Бележки

Тази статия, свързана с математика, все още е мъниче. Помогнете на Уикипедия, като я редактирате и разширите.

Тази статия, свързана с физика, все още е мъниче. Помогнете на Уикипедия, като я редактирате и разширите.