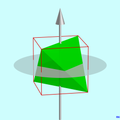
Правилен тетраедър

Правилен тетраедър се нарича равностенен тетраедър, чиито лица са правилни триъгълници (фиг. 1). Той е едно от петте платонови тела.

Тъй като стените му са еднакви равностранни триъгълници, всичките му 6 ръба са равни и всичките му ъгли са по 60°. Правилният тетраедър също е равностранна тристранна пирамида с равностранен триъгълник като нейна основа.

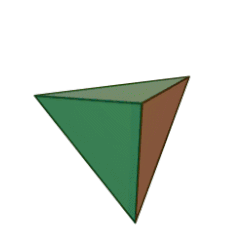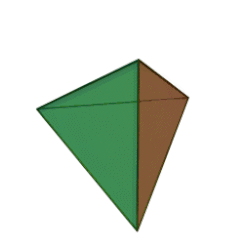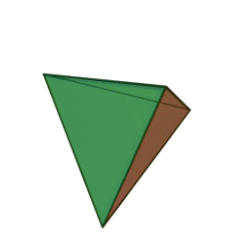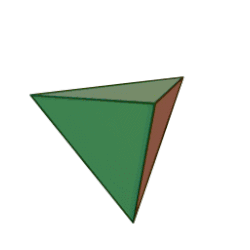
*Фиг. 1*. Анимация на правилен тетраедър

Формули

Ако ръбът на правилен тетраедър е с дължина $a$ , ^[1]

основната повърхнина е: $B={\frac {\sqrt {3}}{4}}{a^{2}}$
околната повърхност е: $S_{ok}=3B={\frac {{3}{\sqrt {3}}}{4}}{a^{2}}$
пълната повърхнина е: $S=4B={\sqrt {3}}a^{2}$
височината е: $h={\sqrt {\frac {2}{3}}}a={{\sqrt {6}} \over 3}a$
обемът e: $V={\frac {\sqrt {2}}{12}}{a^{3}}$ .

Свойства

Свойства на правилния тетраедър:

Всички ръбове на тетраедъра са равни по дължина.
Всички стени на тетраедъра са еднакви равностранни триъгълници, а периметрите и площите им са равни.
Всички двустенни ъгли при ръбовете и всички тристенни ъгли при върховете са равни.
Правилният тетраедър е едновременно ортоцентричен, рамков, равностенен, инцентричен и съизмерим.
Тетраедърът е правилен, ако принадлежи към два вида тетраедри от следните: ортоцентричен, рамков, инцентричен, съизмерим, равностенен.
Тетраедърът е правилен, ако е равностенен и принадлежи към един от следните видове тетраедри: ортоцентричен, рамков, инцентричен, съизмерим.
Октаедър може да бъде вписан в правилен тетраедър, освен това четири (от осем) стени на октаедъра ще бъдат комбинирани с четири стени на тетраедъра, всичките шест върха на октаедъра ще бъдат комбинирани с центровете на шест ръба на тетраедъра.
Правилният тетраедър се състои от един вписан октаедър (в центъра) и четири тетраедъра (във върховете), а ръбовете на тези тетраедри и октаедъра са половината от размера на ръбовете на правилния тетраедър.
Правилен тетраедър може да бъде вписан в куб по два начина, като четирите върха на тетраедъра са подравнени с четирите върха на куба.
Правилен тетраедър може да бъде вписан в додекаедър, освен това четирите върха на тетраедъра ще бъдат комбинирани с четирите върха на додекаедъра.
Пресичащите се ръбове на правилния тетраедър са взаимно перпендикулярни.

Върховете на правилен тетраедър лежат върху сфера, описана около тетраедъра. Той може също да бъде вписан и в куб (фиг. 3), като ръбовете му са различните диагонали върху срещуположни страни.

*Фиг. 3*. Правилен тетраедър, вписан в куб

Обемът на тетраедъра, вписан в куб е $1/3$ от неговия обем:

V={\frac {a^{3}}{3}}

,

където $a$ е страната на куба. ^[2]

Средното сечение на куба, което е квадрат, се очертава от средите на четири страни на вложения тетраедър. Всичките 6 средни точки задават октаедъра, който е дуален на куба.

От съединяването на средните точки на страните на тетраедъра се получава квадратно сечение (фиг. 4).

Интересни факти

Средните точки на стените на правилен тетраедър също образуват правилен тетраедър.

Съотношенията на:

ръбовете и височините на правилните тетрадри, радиусите на вписаните и описаните сфери са съответно равни на ${\frac {1}{3}}$ ;
повърхностите е равно на ${\frac {1}{9}}$ ;
обемите е равно на ${\frac {1}{27}}$ .

Симетрия

Основна статия: Тетраедрална симетрия

3 двойни оси на симетрия
4 трикратни оси на симетрия
Една от 6-те равнини на симетрия
Една от 3 четирикратно въртящи се огледални оси с въртяща се огледална равнина

Правилният тетраедър или правилен четиристен е едно от петте платонови тела и единственото платоново тяло, което не е точково симетрично и има връх срещу всяка стена. Той има висока симетрия:

4 трикратни оси на въртене (през ъглите и центровете на противоположните странични повърхности),
3 четирикратно въртящи се огледални оси и по този начин също три двойно сгъваеми оси на въртене или три оси на симетрия (през центровете на противоположните ръбове) също
6 равнини на симетрия (всяка през един ръб и перпендикулярна на противоположния ръб).

Общо групата на симетрия на тетраедъра (тетраедричната група) има 24 елемента. Това е симетричната група S₄ (точковата група T_d според символите на Шьонфлис или 43m според символите на Херман – Моген) и причинява всички 4! = 24 пермутации на ъглите или страничните повърхности. Това е подгрупа на групата на октаедъра или групата на куба.

По-конкретно принадлежат към тетраедричната група

12 завъртания (четни пермутации), т.е.

идентичното изображение,
8 завъртания на 120° (4 възможни оси на въртене през ъгъл всяка и центъра на срещуположната триъгълна повърхност, 2 опции за посока на въртене) и
3 завъртания на 180° (оси на въртене през центровете на два противоположни ръба)

както и

12 нечетни пермутации. Това се получава чрез извършване на отражение върху фиксирана равнина на симетрия след всяка от 12-те четни пермутации. Шест от тях също могат да бъдат описани като чисто равнинно отражение, останалите 6 – като ротационни отражения на въртене на 90° около ос, която минава през центровете на два противоположни ръба, и отражение върху равнината, перпендикулярна на тази ос, която е център между двата срещуположни ръба.

Четните пермутации образуват подгрупа на тетраедричната група, така наречената редуваща се група $A_{4}$ (точковата група T или 23). Понякога терминът тетраедрична група се използва само за тях, с изключение на отраженията.

Вижте също

Източници

↑ Harold Scott MacDonald Coxeter. Table I(i) // Regular Polytopes. — Methuen and Co., 1948.
↑ Alsina, C.; Nelsen, R. B. (2015). A Mathematical Space Odyssey: Solid Geometry in the 21st Century. Mathematical Association of America. p.68

[1] Harold Scott MacDonald Coxeter. Table I(i) // Regular Polytopes. — Methuen and Co., 1948.

[2] Alsina, C.; Nelsen, R. B. (2015). A Mathematical Space Odyssey: Solid Geometry in the 21st Century. Mathematical Association of America. p.68

[1]

[2]