Платоново тяло

Платоновите тела (наричани още правилни многостени) са тези изпъкнали многостени, които имат еднакви многостенни ъгли и чиито стени са еднакви правилни многоъгълници.

Съществуват само пет такива многостена.

Обяснението е в това, че за многостенен (телесен) ъгъл с n ръба, сборът от ръбните ъгли трябва да бъде по-малък от 360 градуса, като ъглите на правилните многоъгълници могат да бъдат само 108, 90 и 60 градуса, съответстващи на петоъгълник, четириъгълник и триъгълник. Така в един връх на платоново тяло могат да се срещат три петоъгълника, три четириъгълника, и три, четири или пет триъгълника. Поради тази причина съществуват само пет платонови тела (правилни многостени). Така подредени, те се наричат: додекаедър (дванадесетостен); хексаедър (шестостен), по-често наричан куб; тетраедър (четиристен); октаедър (осмостен) и икосаедър (двадесетостен).

Платоново тяло	Стени	Брой стени	Брой ръбове	Брой върхове	Брой стени през връх	Повърхнина S	Обем V
Тетраедър	триъгълник	4	6	4	3	$S=a^{2}{\sqrt {3}}$	$V={\frac {a^{3}{\sqrt {2}}}{12}}$
Хексаедър (куб)	квадрат	6	12	8	3	$S=6a^{2}\,$	$V=a^{3}\,$
Октаедър	триъгълник	8	12	6	4	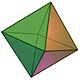$S=2a^{2}{\sqrt {3}}$	$V={\frac {a^{3}{\sqrt {2}}}{3}}$
Додекаедър	петоъгълник	12	30	20	3	$S=3a^{2}{\sqrt {5(5+2{\sqrt {5}})}}$	$V={\frac {a^{3}(15+7{\sqrt {5}})}{4}}$
Икосаедър	триъгълник	20	30	12	5	$S=5a^{2}{\sqrt {3}}$	$V={\frac {5a^{3}(3+{\sqrt {5}})}{12}}$

Свойства

Платоновите тела има множество интересни (нетривиални) свойства.

Тъй като са изградени от правилно разположени правилни многоъгълници, то центровете на стените им също образуват платонови тела. Така центровете на стените на куба образуват октаедър и, обратно, центровете на октаедър образуват куб. Аналогично свойство имат додекаедърът и икосаедърът. При тетраедъра се получава пак тетраедър. Това свойство се описва като 'дуалност' и то е израз на симетрията, присъща на трите различаващи се случая.

За платоновите тела е в сила една обща формула, свързваща броя на елеметите (стени, върхове, ръбове), от които са изградени; записана неформално тя има вида:

стени + върхове = ръбове + 2 .

Числото две е т.нар. 'ойлерова характеристика' на общия клас, в който попадат и платоновите тела. Отношенията на дуалност са свързани също с тази формулата.

История

Правилните многостени стават известни като „(петте) Платонови тела“, тъй като Платон обяснява с тях устройството на вселената. Това е направено в съчинения от него диалог „Тимей“ ^[1] (IV в. пр.н.е.). Там четитрите „стихии“ (земя, вода, въздух, огън) са представени съответно като състоящи се от кубове, икосаедри, октаедри, тетраедри. На оставащия пети многостен, додекаедъра, е приписано представянето на космоса като цяло.

На практика правилни многостени са били известни дълго преди появата на класическите цивилизации^[2]. Схващането им като специален клас обаче е зафиксирано в традицията на питагорейците.

В книга XIII от „Елементи“ на Евклид, са изследвани по-строго техните свойства и е приведено доказателство, че няма други освен вече известните пет^[3].

Интересът към правилните многостени се завръща отчетливо през Ренесанса. В края на XV в. пълният текст на платоновия диалог отново става достъпен. Йохан Кеплер обяснява хелиоцентричния модел предложен от Коперник като помества между орбитите на шестте известни планети платоновите многостени.

Обобщения

Обобщения на платоновите тела се правят по различни начини, а те позволяват и обратното – тяхното схващане като частни случаи. Така в средата на XIX век Людвиг Шлефли намира обобщение за пространство с размерност 4: оказва се, че в този случай са възможни 6 тела – пет от тях са многомерни аналози на платоновите^[4]. За пространства с по-голяма размерност възможните случаи са 3, съответстващи на видовете симетрия, която дуалностите разкриват.

Като обобщение на платоновите тела могат да се разглеждат и тела, чиито стени са правилни многоъгълници от няколко (т.е. един или повече) вида. Тогава към тях се присъединяват архимедовите тела, изграждани с такива стени от 2 или 3 вида: при тях всички ръбове и обемни ъгли остават равни, а симетриите им остават в същите класове.

Бележки

↑ Платон „Диалози“, т. 4, София: „Наука и изкуство“ 1990, с. 508 и сл.
↑ Lloyd D. R, (2012), How old are the Platonic Solids?, BSHM Bulletin: J. of the British Society for the History of Mathematics, 27:3, 131 – 140
↑ Заглавието „Елементи“ е латински еквивалент на гръцкото „стихии“
↑ *Schläfli, Ludwig. Theorie der vielfachen Kontinuität. Zürich, Basel: Georg & Co., 1901, [1852]. ISBN 978-1-4297-0481-6. (на немски)

Вижте също

Външни препратки

Информация за платоновите тела, Wolfram MathWorld
Hart G., Neolithic Carved Stone Polyhedra;

[1] Платон „Диалози“, т. 4, София: „Наука и изкуство“ 1990, с. 508 и сл.

[2] Lloyd D. R, (2012), How old are the Platonic Solids?, BSHM Bulletin: J. of the British Society for the History of Mathematics, 27:3, 131 – 140

[3] Заглавието „Елементи“ е латински еквивалент на гръцкото „стихии“

[4] *Schläfli, Ludwig. Theorie der vielfachen Kontinuität. Zürich, Basel: Georg & Co., 1901, [1852]. ISBN 978-1-4297-0481-6. (на немски)

[1]

[2]

[3]

[4]