Джонсоново тяло
Джонсоново тяло е изпъкнал многостен, чиито стени са правилни многоъгълници, без той да е еднообразен. Възможните видове са 92 и списъкът им е публикуван от Норман Джонсон в 1966 г.[1] По дефиниция не са джонсонови Платоновите и Архимедовите тела, нито призмите или антипризмите – при всички тях върховете са еднотипни (т.е те са едноообразни). Възможни форми за стените ca правилните равнинни фигури с 3,4,5,6,8 или 10 страни. Изискването за изпъкналост ограничава броят на стени, срещащи се във връх, до числата 3, 4 или 5. Номенклатурата на Джонсоновите тела допуска синонимия без да е двусмислена. Употребима е стандартна номерация J1 до J92.
Именуване и Класификация
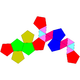
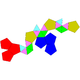
[редактиране | редактиране на кода]Повечето джонсонови тела могат да бъдат видяни като модификации на еднообразните тела изключени от класа. Така например телата с номера J58-61 се получават с построване на петстенни прирамиди, върху някои от стените на додекаедър, която се явява като тяхна основа:
| J58 | J59 | J60 | J61 |
|---|---|---|---|

|

|

|

|
| надстроен додекаедър | пара-дву-надстроен додекаедър | мета-дву-надстроен додекаедър | три-надстроен додекаедър |

|

|
|
|
| додекаедър и петстенна пирамида | |||
Всички джонсонови тела имат триъгълни страни, така че според една възможна класификация те биват разглеждани като комбинациите на този базисен и тип и останалите допустими правилни многоъгълници (4,5,6,8, 10 страни), общо 9 класа:
- 3 : 5 вида
- 3+4 : 24 вида
- 3+5 : 11 вида
- 3+4+5 : 20 вида
- 3+4+6 : 8 вида
- 3+4+8 : 5 вида
- 3+5+10 : 2 вида {J6, J25}
- 3+4+5+6 : 1 вид J92
- 3+4+5+10 : 16 вида
Пълното описание на джонсоновите тела включва номер, наименование, брой върхове (S), ръбове (Е), брой стени, общо и по видове (F и F3-10), симетрия, както е показано в таблицата по долу за първите шест.
| No | Име | Картинка | Tип | S | Е | F | F3 | F4 | F5 | F6 | F8 | F10 | Симетрия |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| J1 | квадратна пирамида | пирамида | 5 | 8 | 5 | 4 | 1 | 0 | 0 | 0 | 0 | C4v | |
| J2 | петстенна пирамида | пирамида | 6 | 10 | 6 | 5 | 0 | 1 | 0 | 0 | 0 | C5v | |
| J3 | шестоъгълен купол | 
|
купол | 9 | 15 | 8 | 4 | 3 | 0 | 1 | 0 | 0 | C3v |
| J4 | осмоъгълен купол | 
|
купол | 12 | 20 | 10 | 4 | 5 | 0 | 0 | 1 | 0 | C4v |
| J5 | десетоъгълен купол | 
|
купол | 15 | 25 | 12 | 5 | 5 | 1 | 0 | 0 | 1 | C5v |
| J6 | десетоъгълна ротонда | 
|
ротонда | 20 | 35 | 17 | 10 | 0 | 6 | 0 | 0 | 1 | C5v |
За 25 от джонсоновите тела може да се намери сфера, върху която да лежат всички техни върхове: J 1 – 6,11,19,27,34,37,62,63,72 – 83. От всичките 92 тела 64 могат да бъдат съставени от присъединяване на тела с правилни многоъгълни стени, докато останалите 28 са несъставни или в този смисъл "прости".[2]
През 1969 г. Виктор Залгалер доказва, че освен изброените от Норман Джонсон 92 тела няма други в същия клас. [3]
Източници
[редактиране | редактиране на кода]- ↑ Johnson, Norman W. Convex polyhedra with regular faces // Canadian Journal of Mathematics 18. 1966. DOI:10.4153/cjm-1966-021-8. с. 169 – 200.
- ↑ Timofeenko, A. V. Junction of Non-composite Polyhedra // St. Petersburg Mathematical Journal 21 (3). 2010. DOI:10.1090/S1061-0022-10-01105-2. с. 483–512.
- ↑ Залгалер, Виктор A. . Выпуклые многогранники с правильными гранями // Зап. Науч. Семин. ЛOMИ Стеклов 2. 1967. с. 1 – 221.
