Вълновод

Вълновóдът е изкуствен или естествен направляващ канал, по който може да се разпространяват електромагнитни или акустични вълни. В този случай потокът от мощност, пренасян от вълната, се концентрира вътре в този канал или в областта на пространството, непосредствено съседна на канала.

В тесния смисъл на думата вълновод се нарича преносна линия с формата на метална тръба или диелектрично стебло, по дължината на които се разпространяват електромагнитни вълни. Те се наричат съответно метални и диелектрични вълноводи. Може да имат различни форми и размери. Делят се на две основни групи: правоъгълни и цилиндрични. Вторите могат да бъдат с кръгло или елиптично напречно сечение. Формата и размерите на напречното сечение определят разпределената индуктивност и разпределения капацитет. ^[1]

Най-често терминът „вълновод“ се отнася до метални тръби, предназначени да предават енергията на електромагнитните вълни в диапазона на СВЧ и КВЧ. Такъв вълновод е преносна линия с една или повече проводими повърхности, с напречно сечение под формата на затворена проводима верига, покриваща областта на разпространение на електромагнитна енергия. ^[2].

Разпространението на вълната по дължината на вълновода става чрез многократно отражение от стените му и интерференция на отразените вълни. ^[3]

Вълноводите могат да се използват за предаване на електромагнитни вълни от дециметровия до оптичния обхват с различни загуби на енергия. Най-голямо приложение намират в диапазона на свръхвисоките честоти, затова са основен вид преносни линии за сантиметрови вълни. ^[1]

Моментна картина на напрeгнатостта на електричното поле Е на вълна тип Н₁₀ в извивка на правоъгълен метален вълновод.

Историческа справка

Първата конструкция за предаване на вълни е предложена от английския физик Джоузеф Джон Томсън през 1893 г., а първи е проверил експериментално нейния принцип английския физик и изобретател Оливър Лодж през 1894 г. Първият математически анализ на хода на електромагнитните вълни в метален цилиндър е извършен от британския физик и механик лорд Релей през 1897 г. ^[4]. В процеса на задълбочено проучване на звукови вълни (повърхностни акустични вълни) лорд Релей публикува пълен математически анализ на принципа на тяхното разпространение в своето фундаментално изследване „Теория на звука“ ^[5].

По-късно, през 20-те години на ХХ век, започва изследването на диелектрични вълноводи (включително оптични влакна). Няколко учени, сред които най-известните са британският физик и механик лорд Релей, немският теоретичен физик и математик Арнолд Зомерфелд, както и холандският физик Петер Дебай ^[6]. Фундаменталните изследвания довеждат до факта, че през 60-те години стъкловлакната започват да привлича специално внимание поради възникващите възможности за използването им за предаване на данни и връзка.

Видове

Според материала

Метални (екранирани)

без запълнение
частично запълнени с диелектрик

Екранираният вълновод има добре отразяващи стени за разпространението на вълната в него, така че вълновият поток от мощност е концентриран във вълновода. По правило такива вълноводи са направени под формата на кухи тръби или запълнени със среда със специално подбрани параметри. Напречното сечение на тези тръби има формата на правоъгълник, кръг, елипса, което е свързано с по-голяма структурна простота, въпреки че се използват и вълноводи за други цели с други форми на напречно сечение. За да не се отразява вълната в обратна посока, вълноводът се изработва еднороден: формата и размерите на напречното сечение, както и физическите свойства на материалите, трябва да бъдат постоянни по дължината на вълновода. Тъй като вълната се отразява от стените на екранирания вълновод, в напречна посока се появява стояща вълна с определен състав на типовете колебания (модовете).

За предаване на електромагнитни вълни се използват метални тръби, кухи или напълнени с диелектрик. Терминът радиочестотен вълновод (на английски radiofrequency guide, обозначаване RG) подчертава предназначението и разликата от проводниците за пренос на постоянен ток и ток с промишлена честота, както и от нискочестотни комуникационни кабели. Метални вълноводи и твърди коаксиални линии с прорези в екрана служат за изграждане на вълноводно-процепни и коаксиално-процепни антени.

Екранираните вълноводи също включват акустични вълноводи, това са тръби с доста твърди стени, например метални или пластмасови. В такива вълноводи акустичните вибрации се разпространяват в газа, изпълващ вълновода, обикновено във въздуха. Преди са се използвали широко на кораби и други плавателни съдове под името „разговорни тръби“.

Почти всички видове вълноводи могат да се считат за разновидности на дълги предавателни линии, тоест такива, чиято дължина значително надвишава дължината на разпространяващата се в тях вълна λ или е сравнима с нея, а напречните ѝ размери са по-малки от дължината на вълната.

Диелектрични (неекранирани)

При открити (неекранирани) вълноводи локализацията на полето обикновено се причинява от явлението пълно вътрешно отражение от границата между две среди (в диелектрични радиовълноводи и оптични влакна) или от области с плавно променящи се средни параметри (например атмосферен вълновод, подводен звуков канал, градиентно оптично влакно). Полето е локализирано главно вътре в специално проектирания за този участък напречен разрез на вълновода и бързо намалява извън тази област. Поради това вълната се канализира във вълновода. Отворените плоски оптични вълноводи в интегрално изпълнение се използват за изграждане на различни интегрирани оптоелектронни устройства.

Акустичните отворени вълноводи служат като основа за устройства, базирани на повърхностни акустични вълни; в такива вълноводи, ултразвукова вълна се разпространява по границата между две среди с различни акустични свойства.

Според формата и напречното сечение

правоъгълни
П-образни
Н-образни
цилиндрични
- кръгли
- елиптични

Според честотния диапазон

радиовълноводи – стандартните радиовълноводи се използват за честоти от 320 MHz до 330 GHz (от 93,75 cm до 0,909 mm)

Частни случаи на радиовълноводи са атмосферните вълноводи:
1) тропосферeн вълновод – квазихоризонтален слой в тропосферата, разположен на малка височина над земната (водната) повърхност, в който радиовълните с достатъчно висока честота могат да се разпространяват като в диелектричен вълновод (тоест като в предавателна линия) с много малко затихване;
2) йоносферeн вълновод – квазихоризонтален слой от атмосферата, разположен на височина от земята до най-долния йоносферен слой D, в който дългите радиовълни могат да се разпространяват като в диелектричен вълновод (тоест като в предавателна линия) на много големи разстояния чрез многократно отражение от земята и йоносферата;

световоди: оптични влакна, интегрални оптични вълноводи.

Анализ на процесите във вълноводите

Анализ на процесите в предавателните линии се извършва чрез решаване на електродинамична задача. За вълноводите това става посредством решаване на основните уравнения на електродинамиката – уравненията на Максуел. Решенията представляват математически изрази за напрегнатостите на електрическото и магнитно поле Е и Н. За целта се използват тримерни координатни системи:

В правоъгълния вълновод – правоъгълна координатна система Oxyz. Оста х е по широката страна, оста y е по тясната страна, а оста z – по дължината на вълновода. Равнината на широката стена xOz, в която са разположени магнитнити силови линии, се нарича Н-равнина. Равнината на тясната стена уOz, в която са разположени електричните силови линии, се нарича Е-равнина. Равнината на напречното сечение хOу, която е перпендикулярна на посоката на разпространение по надлъжната ос z, определена от вектора на Пойнтинг, се нарича напречна равнина или равнина на Пойнтинг. Векторите на електрическото и магнитното полета Е и Н се разлагат на 3 съставни: Е_х, Е_у, Е_z, Н_х, Н_у и Н_z. Те се описват с тригонометрични функции.
В цилиндричния вълновод – цилиндрична координатна система Orφz.

Равнината на напречното сечение rOφ, която е перпендикулярна на посоката на разпространение по надлъжната ос z, определена от вектора на Пойнтинг, се нарича напречна равнина или равнина на Пойнтинг. Всяка точка от напречното сечение се определя от радиус-вектора r, изразяващ разстоянието до нея от координатното начало О в центъра на сечението и от ъгловата координата φ. Всяка точка от надлъжно сечение през произволен ъгъл φ се определя от радиус-вектора r, изразяващ разстоянието до нея от оста на цилиндъра z и надлъжната координата z от координатното начало О на цилиндъра. Векторите на електрическото и магнитното полета Е и Н се разлагат на 3 съставни: Е_r, Е_φ, Е_z, Н_r, Н_φ и Н_z. Те се описват с Беселови функции.

Типове вълни във вълноводите

Типовете вълни се наричат модове. Определят се от структурата на полето.

Напречни електрични вълни или магнитни вълни. Наричат се ТЕ-вълни или Н-вълни. Електричното им поле има само напречни съставни Е_х и Е_у (в напречната равнина спрямо посоката на разпространение) и няма надлъжна съставна Е_z (по посоката на разпространение). Магнитното им поле има надлъжна съставна Н_z.
Напречни магнитни вълни или електрични вълни. Наричат се ТН-вълни или Е-вълни. Магнитното им поле има само напречни съставни Н_х и Н_у (в напречната равнина спрямо посоката на разпространение) и няма надлъжна съставна Н_z (по посоката на разпространение). Електричното им поле има надлъжна съставна Е_z. ^[1]

В металните вълноводи могат да се разпространяват Н-вълни и Е-вълни. Напречна електромагнитна вълна (ТЕМ-вълна), т.е. такава, която едновременно няма надлъжни съставни и на електричното, и на магнитното поле, не съществува. Тя може да се разпространява в двупроводните линии.

В диелектричните вълноводи освен посочените, могат да се разпространяват и вълни, които съдържат и шестте компоненти на полето: Е_х, Е_у, Е_z, Н_х, Н_у и Н_z.

Всеки мод се означава с буква Е или Н и 2 индекса: Е_mn или Н_mn. Индексите m и n означават броя на полувълните на полето в определени направления от напречното сечение на вълновода:

В правоъгълния вълновод m е броят на полувълните на полето, които се нанасят по широката страна, а n – по тясната страна на напречното сечение на вълновода. Например, Н₁₀ означава магнитна вълна с 1 полувълна на полето по широката стена а и 0 полувълни (постоянна стойност) по тясната стена b на вълновода.

Структура и разпределение на електричното поле Е на вълни тип Н₁₀, Н₂₀ и Н₃₀ в напречното сечение на правоъгълен вълновод

Силови линии на електричното поле (в червено) и на магнитното поле (в зелено) на основния мод H₁₀ в правоъгълен вълновод.
Силови линии на електричното поле (в червено) и на магнитното поле (в зелено) на основния мод (H₁₁) в кръгъл вълновод.

В цилиндричния вълновод m е броят на полувълните на полето, които се нанасят по периферията (обиколката с дължина 2πR), а n – по радиуса R на вълновода. Например, E₀₁ означава електрична вълна с 0 полувълни (постоянна стойност) на полето по периферията на вълновода и 1 полувълна по радиуса а на вълновода.

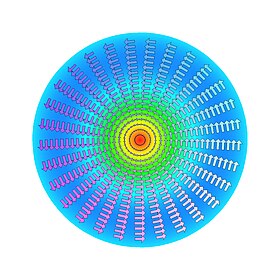
Eлектрично поле на вълна Е₀₁ в кръгъл вълновод. Стрелките показват моментната посока на вектора Е, а големината им и цвета на фона – амплитудата на полето.
Магнитно поле на вълна Е₀₁ в кръгъл вълновод. Стрелките показват моментната посока на вектора Н, а големината им и цвета на фона – амплитудата на полето.

В кръглия цилиндричен вълновод вълните с индекс m=0, т.е. Е₀₁ и Н₀₁ не се изменят по ъгловата координата и, следователно, притежават осева симетрия. Поради това те са пригодни за използване във въртящи се съединения. ^[1]

Eлектрично поле на вълна Н₀₁ в кръгъл вълновод. Стрелките показват моментната посока на вектора Е, а големината им и цвета на фона – амплитудата на полето.
Магнитно поле на вълна Н₀₁ в кръгъл вълновод. Стрелките показват моментната посока на вектора Н, а големината им и цвета на фона – амплитудата на полето.

Дължината на вълната (честотата), при която константата на разпространение става равна на нула, се нарича критична дължина на вълната λ_кр (критична честота f_кр). Това е най-дългата вълна (най-ниската честота), която може да се разпространява във вълновода. Критичната дължина на вълната нараства при увеличаване на размерите на напречното сечение на вълновода. За всеки тип вълна тя е различна и се определя по формулата:

за правоъгълен вълновод

\lambda _{\mathrm {kp,} mn}={\frac {2}{\sqrt {\left({\frac {m}{a}}\right)^{2}+\left({\frac {n}{b}}\right)^{2}}}}={\frac {c}{f_{\mathrm {kp} }}}

,

където а е вътрешният размер на широката страна, а b – вътрешният размер на тясната страна на напречното сечение на вълновода.

за кръгъл вълновод се определят по отделни формули за Е- и Н-вълни:
- за Е-вълни:

\lambda _{\mathrm {kp,} Emn}={\frac {2\pi R}{U_{mn}}}\,

,

където R е вътрешният радиус на цилиндъра, а U_mn е n-ия корен на Беселовата функция от m-ти ред J_m(kr), с която се формулира изразът за напрегнатостта на полето Е и Н за този тип вълна.

- за Н-вълни:

\lambda _{\mathrm {kp,} Hmn}={\frac {2\pi R}{U'_{mn}}}\,

,

където R е вътрешният радиус на цилиндъра, а U_mn е n-ия корен на първата производна J'_m(kr) на Беселовата функция от m-ти ред за този тип вълна; $k={\frac {2\pi }{\lambda }}\,$ e вълновото число.

Корените се получават чрез приравняване на Беселовата функция или първата ѝ производна на 0 и решаване на получените уравнения. При изчисления се взимат от готови таблици за съответните стойности на m и n. ^[1]

Този тип вълна, който има най-голяма критична дължина на вълната, се нарича основен тип вълна. За металния правоъгълен вълновод това е Н₁₀, а за кръглия цилиндричен – Н₁₁. Останалите се наричат висши типове вълни (модове). Обикновено работният мод е един и това е основният мод, но в някои случаи може да са и повече, най-често два или три. Наличието на останалите, неработни модове е нежелателно, защото води до загуби на енергия. Неразпространението им се осигурява чрез подбор на определено съотношение между дължината на вълната (честотата) и напречните размери на вълновода или чрез филтри.

В правоъгълния вълновод критичните дължини λ_кр за вълните Е_mn и Н_mn с еднаква двойка индекси m и n съвпадат. В кръглия вълновод колебанията Е и Н с еднаква двойка индекси m и n имат различни λ_кр. ^[1]

Параметри

Константа на разпространение и работен диапазон

Ако Z(z) е функцията на надлъжното разпределение на полето, параметърът

\gamma ={\sqrt {{\frac {1}{Z(z)}}\cdot {\frac {d^{2}Z(z)}{dz^{2}}}}}=const

се нарича константа на разпространение. В общия случай тя е комплексна величина:
$\gamma =\alpha +j\beta$ ,
където $\alpha$ е коефициентът на затихване, а $\beta$ – фазовата константа.

Константата на разпространение зависи от честотата (дължината на вълната):

1) За да се разпространява по дължината на вълновода бягаща вълна с постоянна амплитуда, пренасяща енергия, константата на разпространение трябва да бъде чисто имагинерна величина $\gamma =j\beta$ и да няма затихване $\alpha =0$ , Това се постига при дължина на вълната под критичната (честота над критичната): λ < λ_кр (f > f_кр).

2) При критична честота/дължина на вълната (f = f_кр, λ = λ_кр) $\gamma =0$ и по дължината на вълновода има реактивно поле с постоянна амплитуда, което не пренася енергия.

3) При дължина на вълната над критичната (честота под критичната): λ > λ_кр (f < f_кр) константата на разпространение е чисто рeална величина, изцяло равна на коефициента на затихване във вълновода: $\gamma =\alpha$ и $\beta =0$ . Полето бързо затихва и във вълновода вълна не се разпространява.

Теоретично във вълновода могат да се разпространяват вълни с дължина под критичната (честота над критичната) λ < λ_кр (f > f_кр). Работният диапазон се определя от условието за разпространение на необходимия тип вълна.

При зададени размери на вълновода, за да се разпространява само основния мод, дължината на вълната трябва да бъде в границите:

за правоъгълния вълновод (Н₁₀) – a < λ < 2a, където а е вътрешният размер на широката стена;
за кръглия вълновод (Н₁₁) – 2,613R < λ < 3,413R, където R е вътрешният радиус на цилиндъра.

Когато се налага да се разпространява само някой от висшите модове, се избира дължина на вълната λ < λ_кр за този мод и λ > λ_кр за следващия висш мод с по-малка λ_кр. За неразпространение на по-нисшите модове (с по-голяма λ_кр) се поставят модови режекторни филтри.

Коефициент на дисперсия

В общия случай

d={\sqrt {\varepsilon '-{\left({\frac {\lambda }{\lambda _{\mathrm {kp} }}}\right)^{2}}}},

където $\,\varepsilon '\,$ е относителната диелектрична проницаемост на запълващата материя. За въздушно запълване (кух вълновод) $\,\varepsilon '=1\,$ и

d={\sqrt {1-{\left({\frac {\lambda }{\lambda _{\mathrm {kp} }}}\right)^{2}}}}.

Дължина на вълната във вълновода

Поради дисперсията дължината на вълната във вълновода е по-голяма от тази в свободното пространство λ_в > λ:

\lambda _{\mathrm {b} }={\frac {\lambda }{d}}

Фазова и групова скорост

Фазова скорост е скоростта на изменение на фазата на полето:

v_{\mathrm {f} }={\frac {c}{d}}

.

Групова скорост е скоростта на разпространение на енергията на полето:

v_{\mathrm {rp} }=cd

.

Вълново съпротивление

За Н-вълни

Z_{\mathrm {c,H} }={\frac {Z_{\mathrm {0} }}{d}}

За Е-вълни

Z_{\mathrm {c,E} }={Z_{\mathrm {0} }}{d}

,

където $Z_{\mathrm {0} }=120\pi =377\,\Omega$ е вълновото съпротивление на свободното пространство.

За основните типове вълни в различни вълноводи стойността на вълновото съпротивление е около 500 Ω.

Мощности

Мощност, пренасяна от типа вълна. Пропорционална е на напречното сечение на вълновода.
Пределна мощност – мощността, при която във вълновода настъпва електрически пробив. Това става при пределна напрегнатост на полето, която има най-голяма стойност за въздух – E_пр=30 kV/cm. При твърд диелектрик намалява с увеличаване на относителната диелектрична проницаемост ε'. Затова пределната мощност е най-голяма при кух вълновод, запълнен с въздух. Трябва обаче да се отчита, че пределна напрегнатост на полето във въздуха намалява с намаляване на атмосферното налягане. Това е важно при работа на вълновода в техника на въздушни и космически обекти - с увеличаване на височината нараства вероятността за електрически пробив. За целта вълноводната линия е херметизирана и в нея се поддържа повишено налягане с компресор.
Допустима работна мощност – избира се от 3 до 5 пъти по-малка от пределната.

Предимства

малки загуби – нямат вътрешен проводник и допълнителна изолация.
няма смущения и допълнително излъчване на енергия.
предават се вълни с по-голяма мощност.
ниски загуби от скин-ефекта. ^[3]
вероятността за електрически пробив е по-малка от тази при двупроводните линии поради отсъствието на втори проводник. Пробив може да настъпи между стените на вълновода ако напрегнатостта на полето в него достигне и надвиши пределната си стойност за съответната среда на разпространение. Тя е най-голяма за въздух – E_пр = 30 kV/cm. За останалите диелектрици намалява пропорционално на корен квадратен от тяхната относителна диелектрична проницаемост ε'. ^[1]

Проектиране

Вълноводите се изработват с размери, определени от международни стандарти. По принцип (но не винаги) стандартните вълноводи са проектирани така:

честотните ленти на съседните по размери вълноводи частично се припокриват в краищата си;
долната граница на лентата е приблизително 30 % по-висока от критичната честота на вълновода;
горната граница на лентата е приблизително 5 % по-ниска от критичната честота на следващия мод от по-висок ред;
размерите на широката и тясна страна на правоъгълните вълноводи са в отношение a : b = 2 ÷ 2,3.

Първото условие осигурява използването на алтернативен вълновод в краищата на честотната лента. Второто условие ограничава дисперсията – явление, при което скоростта на разпространение е функция на честотата. Също така ограничава загубите на единица дължина (коефициента на затихване α. Третото условие не позволява разпространението на висши типове вълни. Четвъртото условие осигурява двойна честотна лента λ_max ≈ 2λ_min. При кръглите вълноводи най-високата възможна ширина на честотната лента, позволяваща да се разпространява само един тип вълна (мод), е само 1,3601 : 1.

Таблица на стандартните правоъгълни вълноводи

По-долу е дадена таблицата на стандартните правоъгълни вълноводи. В името на вълновода WR означава правоъгълен вълновод, а числото е вътрешният размер a на широката страна на вълновода в стотни от инча (0,01 инча = 0,254 mm), закръглена до най-близката стотна от инча.

Стандартни размери на правоъгълен вълновод
Име на вълновода			Име на честотния диапазон	Препоръчителна работна честотна лента (GHz)	Критична честота на основния мод (GHz)	Критична честота на следващия мод (GHz)	Вътрешни размери на отвора на вълновода a х b
IEC	RCSC ^*	EIA	Име на честотния диапазон	Препоръчителна работна честотна лента (GHz)	Критична честота на основния мод (GHz)	Критична честота на следващия мод (GHz)	(inch)	(mm)
R3	WG0.0	WR2300		0,32 — 0,45	0,257	0,513	23,000 × 11,500	584,20 × 292,10
R4	WG0	WR2100		0,35 — 0,50	0,281	0,562	21,000 × 10,500	533,40 × 266,7
R5	WG1	WR1800		0,45 — 0,63	0,328	0,656	18,000 × 9,000	457,20 × 228,6
R6	WG2	WR1500		0,50 — 0,75	0,393	0,787	15,000 × 7,500	381,00 × 190,5
R8	WG3	WR1150		0,63 — 0,97	0.513	1,026	11,500 × 5,750	202,10 × 146,5
R9	WG4	WR975	UHF/L	0,75 — 1,15	0,605	1,211	9,750 × 4,875	247,7 × 123,8
R12	WG5	WR770		0,97 — 1,45	0,766	1,533	7,700 × 3,850	195,6 × 97,79
R14	WG6	WR650	L (чaст)	1,15 — 1,72	0,908	1,816	6,500 × 3,250	165,1 × 82,55
R18	WG7	WR510	LA	1,45 — 2,20	1,157	2,314	5,100 × 2,550	129,5 × 64,77
R22	WG8	WR430		1,72 — 2,60	1,372	2,745	4,300 × 2,150	109,2 × 54,61
R26	WG9A	WR340	LS	2,20 — 3,30	1,736	3,471	3,400 × 1,700	86,36 × 43,18
R32	WG10	WR284	S (чaст)	2,60 — 3,95	2,078	4,156	2,840 × 1,340 ^†	72,14 × 34,94
R40	WG11A	WR229	A	3,30 — 4,90	2,577	5,154	2,290 × 1,145	58,17 × 29,08
R48	WG12	WR187	G	3,95 — 5,85	3,153	6,305	1,872 × 0,872 ^†	47,55 × 22,2
R58	WG13	WR159	C	4,90 — 7,05	3,712	7,423	1,590 × 0,795	40,38 × 20,2
R70	WG14	WR137	J	5,85 — 8,20	4,301	8,603	1,372 × 0,622 ^†	34,90 × 15,8
R84	WG15	WR112	H	7,05 — 10,00	5,260	10,520	1,122 × 0,497 ^†	28,50 × 12,6
R100	WG16	WR90	X	8,20 — 12,40	6,557	13,114	0,900 × 0,400 ^†	22,9 × 10,2
WR75	WG17	R120	M	10,00 — 15,00	7,869	15,737	0,750 × 0,375	19,1 × 9,53
R140	WG18	WR62	P (Ku)	12,40 — 18,00	9,488	18,976	0,622 × 0,311	15,8 × 7,90
R180	WG19	WR51	N	15,00 — 22,00	11,572	23,143	0,510 × 0,255	13,0 × 6,48
R220	WG20	WR42	K	18,00 — 26,50	14,051	28,102	0,420 × 0,170 ^†	10,7 × 4,32
R260	WG21	WR34	—	22,00 — 33,00	17,357	34,715	0,340 × 0,170	8,64 × 4,32
R320	WG22	WR28	R (Ka)	26,50 — 40,00	21,077	42,154	0,280 × 0,140	7,11 × 3,56
R400	WG23	WR22	Q	33,00 — 50,00	26,346	52,692	0,224 × 0,112	5,68 × 2,84
R500	WG24	WR19	U	40,00 — 60,00	31,391	62,782	0,188 × 0,094	4,78 × 2,39
R620	WG25	WR15	V	50,00 — 75,00	39.875	79,750	0,148 × 0,074	3,76 × 1,88
R740	WG26	WR12	E	60,00 — 90,00	48,373	96,746	0,122 × 0,061	3,10 × 1,55
WR10	WG27	R900	W	75,00 — 110,00	59,015	118,030	0,100 × 0,050	2,54 × 1,27
R1200	WG28	WR8	F	90,00 — 140,00	73,768	147,536	0,080 × 0,040	2,03 × 1,02
R1400	WG29	WR6, WR7, WR6,5	D	110,00 — 170,00	90,791	181,583	0,0650 × 0,0325	1,65 × 0,826
R1800	WG30	WR5		140,00 — 220,00	115,714	231,429	0,0510 × 0,0255	1,30 × 0,648
R2200	WG31	WR4		172,00 — 260,00	137,243	274,485	0,0430 × 0,0215	1,09 × 0,546
R2600	WG32	WR3		220,00 — 330,00	173,571	347,143	0,0340 × 0,0170	0,864 × 0,432

^* RCSC – Комитет по стандартизация на радиокомпонентите (Radio Components Standardization Committee)

^† По исторически причини външните, а не вътрешните размери на тези вълноводи са в отношение 2:1 /с дебелина на стената WG6 – WG10: 0,08" (2,0 mm), WG11A – WG15: 0,064" (1,6 mm), WG16 – WG17: 0,05" (1,3 мм), WG18 – WG28: 1,04" (1,0 мм)/

За честотите в таблицата по-горе, основното предимство на вълноводите над коаксиалните линии е, че вълноводите поддържат разпространението с по-ниски загуби. За по-ниските честоти размерите на вълновода стават непрактически големи, а за по-високите честоти размерите стават непрактически малки (производственият толеранс става значителна част от размера на вълновода).

Особености при изработването

Задължително е вътрешната повърхност да бъде от метал с голяма проводимост, за да има малка дълбочина на проникване на повърхностния ток. Най-често се правят от бронз, възможно е и от мед или алуминий. За увеличаване на проводимостта и намаляване на загубите вътрешната повърхност може да се покрие със сребро, което допълнително оскъпява крайния продукт.
Вътрешната повърхност трябва да е гладка. Не бива да има неравности, по-големи от 0,8 до 3,2 микрона в зависимост от дължината на вълната. В противен случай се появяват смущения от възникването на висши типове вълни (модове). Затова се лакира.
Критичната дължина на вълната λ_кр определя ограничения на напречните размери на вълновода, изработван или избиран за определена дължина на вълната λ:
- При правоъгълния вълновод, за да се разпространява само основният тип вълна Н₁₀, вътрешният размер на широката стена трябва да бъде в границите λ/2 < a < λ, а на тясната – b < λ/2.
- При кръглия вълновод, за да се разпространява само основният тип вълна Н₁₁, вътрешният радиус на цилиндъра трябва да бъде в границите λ/3,413 < а < λ/2,613. ^[1]

Източници

↑ ^а ^б ^в ^г ^д ^е ^ж ^з А. К. Андреев, А. Д. Лазаров – Предавателни линии и СВЧ устройства, ВТС, 1980 г.
↑ ГОСТ 18238-72. Линии передачи сверхвысоких частот. Термины и определения.
↑ ^а ^б ((en)) (вълноводи Глава 14 - Линии за пренос)
↑ N. W. McLachlan, Theory and Applications of Mathieu Functions, p. 8 (1947) (reprinted by Dover: New York, 1964).(англ.)
↑ The Theory of Sound, by J. W. S. Rayleigh, (1894)(англ.)
↑ Advanced Engineering Electromagnetics Архив на оригинала от 2011-12-22 в Wayback Machine. Архив на оригинала от 2009-05-14 в Wayback Machine., by C. A. Balanis, John Wiley & Sons (1989).(англ.)

[Андреев-1] а ^б ^в ^г ^д ^е ^ж ^з А. К. Андреев, А. Д. Лазаров – Предавателни линии и СВЧ устройства, ВТС, 1980 г.

[ГОСТ-2] ГОСТ 18238-72. Линии передачи сверхвысоких частот. Термины и определения.

[Глава_14-3] а ^б ((en)) (вълноводи Глава 14 - Линии за пренос)

[McLachlan-4] N. W. McLachlan, Theory and Applications of Mathieu Functions, p. 8 (1947) (reprinted by Dover: New York, 1964).(англ.)

[rayleigh-5] The Theory of Sound, by J. W. S. Rayleigh, (1894)(англ.)

[balanis-6] Advanced Engineering Electromagnetics Архив на оригинала от 2011-12-22 в Wayback Machine. Архив на оригинала от 2009-05-14 в Wayback Machine., by C. A. Balanis, John Wiley & Sons (1989).(англ.)

[1]

[2]

[3]

[4]

[5]

[6]