Географска ширина
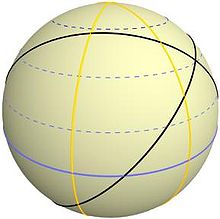
Географската ширина описва положението на дадено място северно (северна ширина) или южно (южна ширина) от екватора. Измерва се в ъгли от 0° на екватора до 90° (на север) и от 0° до -90° (юг) на полюсите. Успоредните на екватора линии се наричат паралели. Географската ширина се използва заедно с географската дължина за определяне на точното местоположение на обекти върху земната повърхност.
Географска ширина на сфера
[редактиране | редактиране на кода]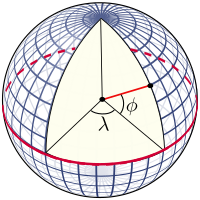
Мрежа на сферата
[редактиране | редактиране на кода]Мрежата се съставя чрез линиите на постоянна географска ширина и дължина, които се построяват спрямо оста на въртене на Земята. Основните отправни точки са полюсите, при които оста на въртене на Земята пресича повърхността. Равнината, в която е разположена оста на въртене, пресича повърхността при меридианите, а ъгълът между коя да е равнина на меридиан и тази на Гринуич (началния меридиан) определя географската дължина. Екваторът има ширина от 0°, докато двата полюса са с ширина съответно от 90° N (северен) и -90° S (южен). Географската ширина на произволна точка е ъгълът между екваториалната равнина и нормалата към повърхността в тази точка – нормалата към повърхността на сферата се чертае по дължина на радиус-вектора.
Ширината, определяна по този начин за сфера, често се нарича сферична ширина, за да се избегне двусмислие с геодезичната ширина и спомагателната ширина.
Известни географски ширини на Земята
[редактиране | редактиране на кода]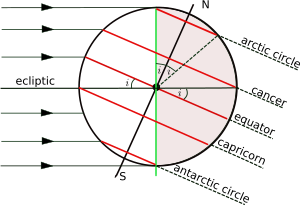
Освен екватора има още четири паралела, които са от особено значение:
Северен полярен кръг 66° 34′ (66.57°) N Тропик на рака 23° 26′ (23.43°) N Тропик на козирога 23° 26′ (23.43°) S Южен полярен кръг 66° 34′ (66.57°) S
Равнината на земната орбита около Слънцето се нарича еклиптика, а равнината, перпендикулярна на оста на въртене на Земята, екваториалната равнина. Ъгълът между еклиптиката и екваториалната равнина образува наклон на оста и често се обозначава с i. Географската ширина на тропичните кръгове е равен на i, а ширината на полярните кръгове е 90° – i. Оста на въртене на Земята се изменя бавно с течение на времето, а използваните стойности тук касаят текущата епоха.
Фигурата вдясно показва геометрията на напречен разрез на равнина, перпендикулярна на еклиптиката и през центъра на Земята, докато Слънцето е в декемврийското слънцестоене над точка от тропика на Козирога. Южните полярни географски ширини под Южния полярен кръг са огрени от слънцето, докато северните географски ширини над Северния полярен кръг са потънали в мрак. Ситуацията се обръща по време на юнското слънцестоене, когато Слънцето е над тропика на рака. Само при географски ширини между двата тропика е възможно Слънцето да застане точно отгоре (в зенит).
При картографските проекции няма универсално правилно относно изобразяването на меридианите и паралелите. Примерите по-долу показват главните паралели върху често използваната Меркаторова проекция и трансверсалния ѝ вариант. При първата паралелите са хоризонтални, а меридианите са вертикални, докато при втората няма точна връзка между паралелите и меридианите – и двете са сложни криви.
| Нормална Меркаторова проекция | Трансверсална Меркаторова проекция | |||
|---|---|---|---|---|
 |
\ |
 |
Меридионално разстояние върху сфера
[редактиране | редактиране на кода]Върху сфера нормалата преминава през центъра ѝ и следователно географската ширина (φ) е равна на ъгъла, образуван в центъра от меридионалната дъга от екватора до изследваната точка. Ако меридионалното разстояние се обозначи с m(φ), тогава
където R е средният земен радиус. R е равен на 6371 km. Не е подходяща по-голяма точност за R, тъй като резултатите с голяма точност биха направили използването на елипсоиден модел неизбежно. С тази стойност за R, меридионалното разстояние на 1 градус географска ширина върху сфера е 111,2 km. Разстоянието на 1 минута географска ширина е 1,853 km, а разстоянието на 1 секунда географска ширина е 30,8 m.
Географска ширина на елипсоид
[редактиране | редактиране на кода]Елипсоиди
[редактиране | редактиране на кода]През 1687 г. Исак Нютон публикува труда Математически начала на натурфилософията, в който той доказва, че въртящо се флуидно тяло със собствена гравитация в равновесие приема формата на сплеснат елипсоид.[1] Резултатът на Нютон е потвърден от геодезичните измервания през 18 век. Сплеснатият елипсоид представлява триизмерна повърхност, създадена от въртенето на елипса около късата си ос.
Много различни отправни елипсоиди са използвани в историята на геодезията. Преди сателитите, те са разделяни, за да се получи добро напасване на геоида върху ограничена площ, но с изобретяването на GPS става практика да се използват отправни елипсоиди (WGS84) с център в масовия център на Земята. Тези геоцентрични елипсоиди обикновено съвпадат до 100 m с геоида. Тъй като географската ширина се определя по отношение на елипсоид, позицията на всяка точка е различна върху всеки елипсоид – не е възможно с точност да се определи географската ширина и дължина на географски обект, без да се уточни използвания елипсоид. Много карти, поддържани от национални служби, се основават на по-стари елипсоиди, така че е нужно да се знае как стойностите на ширината и дължината се преобразуват от един елипсоид към друг. GPS приемниците включват софтуер, който преобразува датуми, свързвайки WGS84 с местния отправен елипсоид.
Геометрия на елипсоида
[редактиране | редактиране на кода]
Формата на елипсоид при завъртане се определя от формата на елипсата, която се върти около късата ѝ ос. Нужни са два параметъра: единият е постоянния екваториален радиус, който е полуголямата ос a, а другият обикновено е (1) полярният радиус на полумалката ос b, (2) първата сплеснатост f или (3) ексцентрицитетът e. Тези параметри са свързани чрез следните връзки:
Много други параметри се появяват в геодезията, геофизиката и картографските проекции, но всичките те могат да се изразят спрямо един или два члена от множеството a, b, f и e. Както f, така и e са малки и често се появяват в разширени редове при изчисления – те са от порядъка на 1300 и 0,08 съответно. Отправните елипсоиди обикновено се определят от полуголямата ос и обратната сплеснатост 1f. Например, определящите стойности за елипсоида WGS84, използван от всички GPS устройства, са:[2]
- a (екваториален радиус): 6 378 137 m точно
- 1f (обратна сплеснатост): 298,257223563 точно
от които се извеждат
- b (полярен радиус): 6 356 752,3142 m
- e2 (ексцентрицитет на квадрат): 0,00669437999014
Разликата между полуголямата и полумалката оси е около 21 km и като част от полуголямата ос се равнява на сплеснатостта. На компютърен екран тя може да бъде изобразена с 300 × 299 пиксела. Това би било трудно различимо от сфера с размери 300 × 300, така че илюстрациите обикновено преувеличават сплеснатостта.
Геодезични и геоцентрични географски ширини
[редактиране | редактиране на кода]
Мрежата на елипсоида се съставя точно по същия начин, както върху сфера. Нормалата в точка от повърхността на елипсоид не преминава през центъра му, освен ако точката не лежи на екватора или на някой от полюсите, но дефиницията на географската ширина остава непроменена като ъгълът между нормалата и екваториалната равнина. Терминологията на географската ширина трябва допълнително да се уточни, за да се разграничат:
- Геодезична ширина – ъгълът между нормалата и екваториалната равнина. Често използвана нотация е φ. Това е определението, което се подразбира, когато се използва думата географска ширина без квалификации.
- Геоцентрична ширина – ъгълът между радиуса (от центъра до точка на повърхността) и екваториалната равнина. Няма стандартна нотация (използват се θ, ψ, q, φ′, φc, φg).
- Сферична ширина – ъгълът между нормалата към сферична отправна повърхност и екваториалната равнина.
Важността от определянето на отправен датум може да се илюстрира чрез прост пример. Върху отправната елиспоида на WGS84, центърът на Айфеловата кула има геодезични координати 48° 51′ 29″ N, 2° 17′ 40″ E. Същите координати, но с датум ED50, определят точка на земята, която е на 140 m от кулата. Така е възможно да се изнамерят различни стойности за географската ширина на кулата, а отправният елипсоид рядко се упоменава.
Вижте също
[редактиране | редактиране на кода]Източници
[редактиране | редактиране на кода]- ↑ Newton, Isaac. Book III Proposition XIX Problem III // Philosophiæ Naturalis Principia Mathematica. с. 407.
- ↑ TR8350.2 // National Geospatial-Intelligence Agency publication. с. 3 – 1.[неработеща препратка]




