Триъгълна призма

Триъгълната призма е призма, на която с основите са триъгълници и има три странични стени. Затова е петостен (пентаедър) с 9 ръба и 6 върха, на който страничните стени в общия случай са успоредници с произволни ъгли. Ако те са наклонени към основите, призмата е наклонена. Възможно е едната странична стена на наклонената призма да е правоъгълник, а другите две да са успоредници – когато наклонът е в направление на височината към страната на основата, която е обща с правоъгълника.

Права триъгълна призма е тази, на която всички странични стени са правоъгълници и са перпендикулярни на основите. Правилна триъгълна призма е тази, на която основите са равностранни триъгълници. Може да бъде наклонена или права. Еднородната триъгълна призма е правилна триъгълна призма с равни ръбове – равностранна триъгълна основа и квадратни страни.

Всички сечения, успоредни на основите, са еднакви триъгълници. Перпендикулярите към страничните стени са в една и съща равнина, която е успоредна на основите при права призма и наклонена към тях при наклонена триъгълна призма.

Полуправилен (еднороднен) многостен

Правата триъгълна призма е полуправилен многостен или по-общо равномерен многостен, ако основата е правилен триъгълник, а страните са квадрати.

Този полиедър може да се разглежда като пресечен триъгълен осоедър, представен от символа на Шлефли t{2,3}. Може да се разглежда и като директно произведение на триъгълник и сегмент, който е представен като {3}x{}.

Групата на симетрия на права призма с триъгълна основа е D_3h от 12-ти ред. Групата на въртене е D₃ от 6-ти ред. Групата на симетрия не съдържа централна симетрия.

Двойственият многостен на триъгълна призма е триъгълна бипирамида. В химията тя се среща под формата на въглеводорода триъгълен призман.

Обем

Обемът на всяка призма е равен на произведението на площта на основата и разстоянието между основите. В случая, когато основата е триъгълна, просто трябва да се изчисли площта на триъгълника и да се умножи по дължината на призмата:

V={\frac {1}{2}}bhl

,

където $b$ е дължината на страната на основата, $h$ е височината на триъгълника и $l$ е разстоянието между основите (височината на призмата).

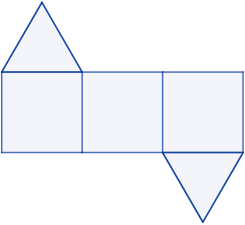
Повърхнина

Околната и пълната повърхнина на триъгълна призма се намират по общите формули за произволна призма, когато основите са триъгълници. Те могат да се получат от формата на разгъната призма, която съдържа 3 успоредника и 2 еднакви триъгълника.

Наклонена триъгълна призма

Нека $a,b$ и $c$ са страните на основите, $l$ е околният ръб, наклонен под ъгъл $\alpha$ към основата, а $d$ е височината на околните стени. Околната (странична) повърхнина $S_{c}$ е сума от площите на 3 успоредника със страни $a,b$ и $c$ , които сключват ъгъл $\alpha$ с общата им страна $l$ .
Площта на основите $B$ е сума от лицата на два еднакви триъгълника и може да се определи по формулата на Херон, а пълната повърхнина $S$ е сума от основната и околната повърхнини.

Околна повърхнина

S_{c}=(a+b+c)d

или

S_{c}=l(a+b+c)\sin {\alpha }

Основна повърхнина

B=2{\sqrt {p(p-a)(p-b)(p-c)}}

,

където $p={\frac {a+b+c}{2}}$ е полупериметърът на триъгълника.

Пълна повърхнина

S=(a+b+c)d+2{\sqrt {p(p-a)(p-b)(p-c)}}

или

S=l(a+b+c)\sin {\alpha }+2{\sqrt {p(p-a)(p-b)(p-c)}}

.

Права триъгълна призма

При правата призма околният ръб е перпендикулярен на основата (α=90°) и съвпада с височината на страничната стена $l=d$ .

Околна повърхнина

S_{c}=(a+b+c)l

Основна повърхнина

B=2{\sqrt {p(p-a)(p-b)(p-c)}}

Пълна повърхнина

S=(a+b+c)l+2{\sqrt {p(p-a)(p-b)(p-c)}}

.

Правилна триъгълна призма

Основните ръбове са равни $a=b=c$ .

Наклонена

Околна повърхнина

S_{c}=3ad

или

S_{c}=3al\sin {\alpha }

Основна повърхнина

S_{c}=a^{2}{\sqrt {3}}

Пълна повърхнина

S=3ad+a^{2}{\sqrt {3}}

или

S=3al\sin {\alpha }+a^{2}{\sqrt {3}}

.

Права

Околна повърхнина

S_{c}=3al

Основна повърхнина

S_{c}=a^{2}{\sqrt {3}}

Пълна повърхнина

S=3al+a^{2}{\sqrt {3}}

.

Еднородна триъгълна призма

Всички ръбове са равни $a=b=c=l$ .

Околна повърхнина

S_{c}=3a^{2}

Основна повърхнина

S_{c}=a^{2}{\sqrt {3}}

Пълна повърхнина

S=(3+{\sqrt {3}})a^{2}

.

Пресечена триъгълна призма

Пресечената права триъгълна призма има пресечена триъгълна повърхност под наклонен ъгъл. ^[1]

Обемът на пресечена триъгълна призма с основна площ $B$ и три височини $h1,h2$ и $h3$ се определя по формулата ^[2]

V={\frac {B(h_{1}+h_{2}+h_{3})}{3}}.

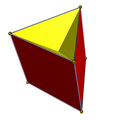
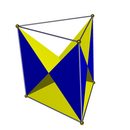
Има пълна D_2h симетрия на сеченията на триъгълна призма без създаване на нови върхове (пресичането на ръбове не се счита за нов връх). Получените многостени имат с 6 стени равнобедрени триъгълници: един многостен, запазващ оригиналните горни и долни триъгълници, и един, запазващ оригиналните квадрати. Двете симетрии на сечението C_3v имат един основен триъгълник, 3 странични самопресичащи се квадрата и 3 равнобедрени триъгълника.