Теорема на Вивиани

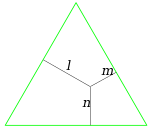
Нека $P$ e вътрешна точка от равнината на един триъгълник. С $d_{a},d_{b},d_{c}$ да означим разстоянията от $P$ до страните $a,b,c$ на триъгълника. Тогава ако с $h_{a},h_{b},h_{c}$ сме означили височините към $a,b,c$, то е изпълнено: $${\frac {d_{a}}{h_{a}}}+{\frac {d_{b}}{h_{b}}}+{\frac {d_{c}}{h_{c}}}=1$$

Доказателство: Очевидно $S_{\triangle }=S_{a}+S_{b}+S_{c}$ където с $S_{k}$, $k=a,b,c$ сме положили лицето на триъгълника с върхове краищата на страната $k$ и точка $P$. В такъв случай следва твърдението на теоремата: $${\frac {S_{a}}{S_{\triangle }}}+{\frac {S_{b}}{S_{\triangle }}}+{\frac {S_{c}}{S_{\triangle }}}={\frac {a.d_{a}}{a.h_{a}}}+{\frac {b.d_{b}}{b.h_{b}}}+{\frac {c.d_{c}}{c.h_{c}}}=1$$

Следствие: Нека с $r$ сме означили радиуса на вписаната окръжност. В такъв случай ако $P$ беше центърът на тази окръжност, то от теоремата на Вивиани следва: $${\frac {1}{h_{a}}}+{\frac {1}{h_{a}}}+{\frac {1}{h_{a}}}={\frac {1}{r}}$$

Вижте също

• Винченцо Вивиани