Собствено движение

Собственото движение на звездата на Барнард от 1985 до 2005 г.

Собствено движение на 61 Лебед

Компоненти на собственото движение върху небесната сфера

Собственото движение е астрономическа мярка за наблюдаваните от Слънчевата система промени в привидното местоположение на звезди или други небесни обекти спрямо абстрактния фон от по-далечни звезди.

Компонентите на собственото движение в екваториалната координатна система (за дадена епоха) се изразяват в посока на ректасцензията (μ_α) и деклинацията (μ_δ). Комбинираната им стойност дава общото собствено движение (μ). Размерността му е ъгъл за време, обикновено арксекунди за година. Познаването на собственото движение, разстоянието и радиалната скорост на дадено небесно тяло позволява да се изчисли неговото истинско движение или скорост в пространството спрямо Слънцето, а чрез координатно преобразуване и спрямо Млечния път. Собственото движение не е изцяло присъщо за небесното тяло, тъй като включва компонент, дължащ се на движението на самата Слънчева система.

Общ преглед

В продължение на векове някои звезди изглеждат сякаш се намират в почти неподвижни позиции една спрямо друга – по този начин те образуват познатите съзвездия. Например Голяма мечка и Южен кръст изглеждат почти по същия начин както преди стотици години. Все пак прецизни и дългосрочни наблюдения показват, че съзвездията изменят формите си, макар и много бавно и че всяка звезда има свое, независимо движение.

Това движение се дължи на придвижването на звездите спрямо Слънцето и Слънчевата система. Слънцето се движи в почти кръгла орбита около центъра на Млечния път със скорост от 220 km/s и описвайки радиус от 8 kPc около центъра, което като цяло е и движението на самия Млечен път в този радиус.

Собственото движение представлява двумерен вектор и като такъв се определя от две величини: позиционния му ъгъл и големината му. Първата величина обозначава посоката на собственото движение върху небесната сфера (0 градуса за движение на север, 90 градуса за движение на изток и т.н.), а втората величина е големината на движението, обикновено изразявана в арксекунди на година (arcsec/yr).

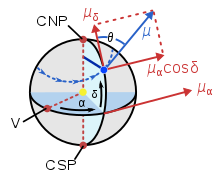
Алтернативно, собственото движение може да се определи като ъгловите промени за година в ректасцензията (μ_α) и деклинацията (μ_δ) на дадена звезда през една и съща епоха.

За обект, придвижващ се от координати (α₁, δ₁) до координати (α₂, δ₂) за време Δt, собственото движение може да се изрази чрез:

$\mu _{\alpha }={\frac {\alpha _{2}-\alpha _{1}}{\Delta t}}\ ,$

$\mu _{\delta }={\frac {\delta _{2}-\delta _{1}}{\Delta t}}\$

Големината на собственото движение μ се получава чрез Питагоровата тероема:

$\mu ^{2}={\mu _{\delta }}^{2}+{\mu _{\alpha }}^{2}\cdot \cos ^{2}\delta \ ,$

$\mu ^{2}={\mu _{\delta }}^{2}+{\mu _{\alpha \ast }}^{2}\ ,$,

където δ е деклинацията. Коефициентът cos²δ компенсира факта, че радиусът от оста на сферата до нейната повърхност се променя чрез cosδ, ставайки например нула при полюса. Следователно компонентът на скоростта, успоредна на екватора за дадена ъглова промяна в α, е по-малък, колкото по̀ на север се намира обектът. Изменението μ_α, което трябва да се умножи по cosδ, за да стане компонент на собственото движение, понякога се нарича собствено движение по ректасцензия, а μ_δ – собствено движение по деклинация.

Ако собственото движение по ректасцензия е преобразувано чрез cosδ, то резултатът се обозначава като μ_α*. Индивидуалните собствени движения по ректасцензия и деклинация се взимат за еквивалентни за прости изчисления на различни други звездни движения. Позиционният ъгъл θ е свързан с тези компоненти чрез:

$\mu \sin \theta =\mu _{\alpha }\cos \delta =\mu _{\alpha \ast }\ ,$

$\mu \cos \theta =\mu _{\delta }\$

Движенията в екваториална координати могат да се превърнат в движения в галактични координати.

История

Собственото движение е предполагано, че съществува от ранните астрономи, но доказателства за него са изнамерени през 1718 г. от Едмънд Халей, който забелязва, че Сириус, Арктур и Алдебаран се намират над половин градус по-далече от позициите им, нанесени от древногръцкия астроном Хипарх около 1850 години по-рано.