Подобие

Показаните в един цвят фигури са подобни.

Подобие е геометричен термин за свойството на геометричните фигури да имат еднаква форма без значение от размерите. Две фигури F₁ и F₂ се наричат подобни, ако между точките им съществува взаимно еднозначно изображение, при което отношенията на разстоянията между всяка двойка съответни точки от фигурите е постоянно неотрицателно число, наречено коефициент на подобие. Терминът е приложим не само за равнинни фигури, но и за тела от триизмерното пространство.

В сила са следните твърдения:

Подобието запазва равни ъглите между съответните линии на фигурите.
Подобие с коефициент k = 1 се нарича еднаквост.
Отношението между периметрите на подобните фигури е равно на коефициента на подобие k.
Отношението между лицата на подобните фигури е равно на k².
Отношението между обемите на подобни тела е равно на k³.
Две фигури, поотделно подобни на трета, са подобни и помежду си.

Подобните фигури е прието да се означават със символа ~ (тилда), например: $\textstyle {\triangle ABC\sim \triangle A'B'C'}$

Подобни триъгълници

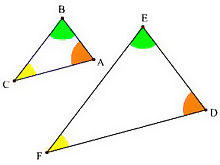
Подобността на триъгълници е понятие в геометрията. Два триъгълника са подобни, ако е на лице един от следните признаци:

Първи признак за подобие на триъгълници

Ако два ъгъла на един триъгълник са съответно равни на два ъгъла от друг триъгълник, то двата триъгълника са подобни.

Втори признак за подобие на триъгълници

Ако две страни на един триъгълник са съответно пропорционални на две страни от друг триъгълник и ъглите между тези страни са равни, то двата триъгълника са подобни.

Трети признак за подобие на триъгълници

Ако страните на един триъгълник са съответно пропорционални на страните на друг триъгълник, то двата триъгълника са подобни.

Четвърти признак за подобие на триъгълници

Ако две страни на един триъгълник са съответно пропорционални на две страни на друг триъгълник и ъглите, лежащи срещу по-големите от тези две страни, са равни, то двата триъгълника са подобни.

От Четвъртия признак за подобие следва Признакът за подобие на правоъгълни триъгълници: Ако хипотенуза и катет от един правоъгълен триъгълник са съответно пропорционални на хипотенуза и катет от друг правоъгълен триъгълник, то двата триъгълника са подобни.

Вижте също