Обхождане в ширина

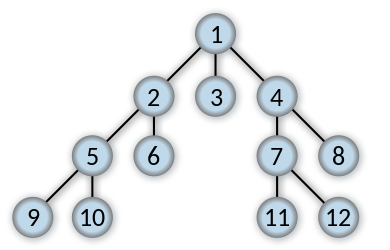
В теорията на графите, обхождането в ширина е начин за търсене в граф, когато търсенето се ограничава до две основни операции:

посещаване и достъпване на разклонение от графа;
получаване на достъп до съседите на посещаваното в даден момент разклонение.

Обхождането в ширина започва от главното разклонение и достъпва всички съседни разклонения. За всяко едно от тези съседни разклонения, проверява техните съседни разклонения, които не са били посетени и така нататък.

Алгоритъм

Алгоритъмът използва структурата опашка, за да съхранява междинните резултати, като пресича графа по следния начин.

Добавя (enqueue) към опашката главното разклонение
Премахва (dequeue) от опашката разклонение и го претърсва, ако търсеният елемент е намерен в това разклонение търсенето се прекратява и се връща резултата.
В противен случай добавя (enqueue) всички наследници (преки дъщерни разклонения), които все още не са открити.
Ако опашката е празна и всяко разклонение от графа е било претърсено търсенето се прекратява и се връща, че търсеното не е било намерено.
Ако опашката не е празна се повтаря стъпка 2.

Забележка: Използването на стек вместо опашка имплементира алгоритъмът – Обхождане в дълбочина.

Псевдокод

Вход: A граф G и главно разклонение v на G

1  начин на действие обхождане в ширина(G,v):
2      създаване на опашкаQ
3      добавяне на v в Q
4      отбелязваме v
5      докато Q не е празна:
6          t ← Q.dequeue() (премахване)
7          ако t това, което търсим:
8              връщаме t
9          за всички edges e in G.adjacentEdges(t) прави
10             u ← G.adjacentVertex(t,e)
11             ако u не е маркиран:
12                  маркираме u
13                  вмъкваме (enqueue) u в Q
14     връщаме none

Характеристики

Заемана памет

Когато броят на върховете на графа е известен предварително и вече добавените в опашката върхове се знаят, запазени в допълнителна структура, сложността може да се изрази с израза $O(|V|)$ , където $|V|$ е множеството от върхове. Ако графът е представен като списък на съседство, той заема $\Theta (|V|+|E|)$ памет, докато представен като матрица на съседство заема $\Theta (|V|^{2})$ памет.

Време на изпълнение

Времето на изпълнение може да се представи с израза $O(|V|+|E|)$ , тъй като всеки връх и „път“ между два съседни върха ще бъде проверен.

Забележка:  $O(|E|)$  може да има стойности между  $O(|V|)$  и  $O(|V|^{2})$ , в зависимост от това, колко сгъстен е дадения граф 
(ако приемем, че графът е свързан).

Употреба

Обхождането в ширина може да бъде използван за решаването на много проблеми в теорията на графите, например:

Намиране на всички разклонения в рамките на един свързан компонент
Копиране на колекции, алгоритъм на Ченей
Намиране на най-краткия път между две разклонение U и V (дължината на пътя е броя на крайните елементи)
Тестване на граф за двучастичност (bipartiteness)

Намиране на свързани компоненти

Обхождането в ширина достига наборът от разклонения чрез свързаните компоненти съдържащи се в първото разклонение.

Тестване за двучастичност

Алгоритъмът за обхождане в ширина може да бъде използван за тестване на двучастичност, като търсенето започне от произволен връх и дадени редуващи се етикети за вече посетените върхове по време на търсенето. Етикет със стойност 0 получава началния връх, 1 получават всичките му съседи, 0 – съседите на съседите на началния връх и така нататък. Ако в даден момент се достигне до връх, който има съсед (посетен) със същия етикет като този връх, то графа не е двустранен. Ако търсенето приключи, без намиране на такъв връх, тогава графът е двустранен.

Реализация

Реализация на обхождане в ширина в Java

Class Node { // създаване на клас за разклоненията

    Char data;
    Public Node(char c) {
        this.data=c;
    }

    public void bfs(){
        Queue q=new LinkedList(); // създаване на опашка
        q.add(this.rootNode);  // добавяне не на главното разклонение към опашката
        printNode(this.rootNode);
        rootNode.visited=true;  // отбелязване на разклонението като посетено
        while(!q.isEmpty()){    // while цикъл докато опашката е пълна
           Node n=(Node)q.remove();  // премахване на разклонението
           Node child=null;
           while((child=getUnvisitedChildNode(n))!=null){  // ако премахнатото разклонение има не посетени дъщерни разклонения
                                                         // ги отбелязваме като посетени и ги добавяме към опашката
                  child.visited=true;
                  printNode(child);
                  q.add(child);
           }
       }
       //Clear visited property of nodes
       clearNodes();
    }
}

Реализация на обхождане в ширина в C#

using System;
using System.Collections.Generic;

/// <summary>
/// Имплементиране на разклонение
/// </summary>
/// <typeparam name="T">the type of the values in nodes</typeparam>
public class TreeNode<T>
{
      // Съдържа стойността на разклонението
      private T value;

      // Показва дали разклонението има родител
      private bool hasParent;

      // Съдържа дъщерните разклонения
      public List<TreeNode<T>> Children;

      /// <summary>
      /// Конструкторът на класът TreeNode
      /// </summary>
      /// <param name="value">стойността на разклонението</param>
      public TreeNode(T value)
      {
            if (value == null)
            {
                  throw new ArgumentNullException(
                        "Cannot insert null value!");
            }
            this.value = value;
            this.children = new List<TreeNode<T>>();
      }

      /// <summary>
      ///Стойността на разклонението
      /// </summary>
      public T Value
      {
            get
            {
                  return this.value;
            }
            set
            {
                  this.value = value;
            }
      }
      public bool IsVisited {get;set;}
}
...
public static int BFS(TreeNode start, TreeNode end) // създаваме метод, който приема като параметри стартовото и крайното разклонение
{
    Queue<TreeNode> queue = new Queue<TreeNode>(); // създаваме си опашка от тип разклонение
    queue.Enqueue(start);                         // добавяме към опашката първото разклонение

    while (queue.Count != 0)               // пускаме цикъл докато опашката е пълна
    {
        TreeNode CurrentNode = queue.Dequeue();  // изваждаме от опашката дадено разклонение
        CurrentNode.IsVisited = true;        // отбелязваме го като посетено

        foreach (Node Child in CurrentNode.Children.Keys)  // претърсваме всички дъщерни разклонения на избраното
        {
            if (Child.IsVisited == false)                 // проверяваме дали е посетено
            {
                Child.IsVisited = true;               // ако не е, го отбелязваме като посетено
                if (Child == end) return 1;           // ако няма повече разклонения връщаме 1
            }
            queue.Enqueue(Child);                    // ако е посетено го добавяме към опашката
        }
    }
    return 0;                                      // ако търсенето не даде резултат връщаме 0
}

Източници

Тази страница частично или изцяло представлява превод на страницата Breadth-first search в Уикипедия на английски. Оригиналният текст, както и този превод, са защитени от Лиценза „Криейтив Комънс – Признание – Споделяне на споделеното“, а за съдържание, създадено преди юни 2009 година – от Лиценза за свободна документация на ГНУ. Прегледайте историята на редакциите на оригиналната страница, както и на преводната страница, за да видите списъка на съавторите.

ВАЖНО: Този шаблон се отнася единствено до авторските права върху съдържанието на статията. Добавянето му не отменя изискването да се посочват конкретни източници на твърденията, които да бъдат благонадеждни.