Обща теория на относителността
За информацията в тази статия или раздел не са посочени източници. Въпросната информация може да е непълна, неточна или изцяло невярна. Имайте предвид, че това може да стане причина за изтриването на цялата статия или раздел. |
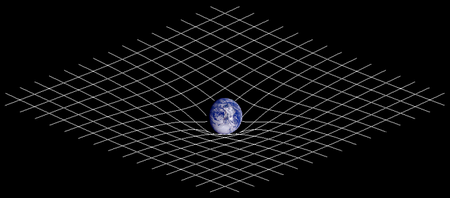
Общата теория на относителността (ОТО) е геометрична теория за гравитацията, публикувана от Алберт Айнщайн през 1915 година. Тя е общоприетият в съвременната физика възглед за характера на гравитацията. Теорията обединява специалната теория на относителността с нютоновия закон за всеобщото привличане и описва гравитацията като геометрично свойство на пространство-времето. В частност, изкривяването на пространство-времето е пряко свързано с тензора енергия-импулс, който зависи от количествата материя и енергия. Тази зависимост е изразена чрез уравненията на Айнщайн, система от частни диференциални уравнения.
Много предвиждания на общата теория на относителността се различават значително от тези на класическата физика, особено във връзка с хода на времето, геометрията на пространството, движението на телата при свободно падане и разпространението на светлината. Примери за такива разлики са гравитационното забавяне на времето, гравитационното червено отместване на светлината и ефекта на Шапиро. Предвижданията на общата теория на относителността се потвърждават от всички наблюдения и експерименти. Макар че не е единствената теория за гравитацията, тя е най-простата, която съответства напълно на експерименталните данни. Въпреки това, общата теория на относителността има и някои непълноти, най-важната от които е нейното съгласуване с квантовата механика, което би създало пълна и последователна теория на квантовата гравитация.
Общата теория на относителността има важни последствия за астрофизиката. Тя подсказва, че в края на развитието си масивните звезди могат да се превърнат в черни дупки, области от пространството, в които пространство-времето е толкова изкривено, че нищо не може да ги напусне. Изкривяването на светлината от гравитацията може да създаде гравитационни лещи, при които се наблюдава повече от един образ на един и същ астрономически обект. Теорията предсказва и наличието на гравитационни вълни, които впоследствие са измерени непряко, а опитите за прякото им наблюдение са основната цел на проекта LIGO. В допълнение към това, общата теория на относителността е основата на съвременните космологични модели на постоянно разширяващата се Вселена.
Основни принципи
[редактиране | редактиране на кода]Общата относителност се основава на група съществени принципи, които определят нейната разработка.
- Общ принцип на относителността: Законите на физиката са еднакви за всички наблюдатели (ускоряващи се или не).
- Принцип на общата ковариантност: Законите на физиката запазват формата си във всички координатни системи.
- Принципът, че Инерциалното движение е движение по геодезични линии: 'Мировите' (траекториите в пространство-времето) линии на частици неповлияни от физически сили са време-подобни или нулеви геодезични линии на пространство-времето.
- Принцип на локална Лоренцова инвариантност: Законите на Специалната относителност са в сила локално за всички инерциални наблюдатели.
- Пространство-времето е изкривено: Това обяснява как свободното падане може да се представи като инерциално движение, докато за масивно тяло, свободното падане е ускорение на тела към центъра на първото.
- Кривината на пространство-времето се създава от тензор на енергията и импулса в пространство-времето: Това в общата относителност се описва от Уравненията на Айнщайн за Полето.
(Принципът на еквивалентността, който е изходна точка в изграждането на общата теория на относителността, завършва като следствие на теорията и на принципа, че инерциалното движение е по 'геодезични линии').
Уравнения на Айнщайн за полето
[редактиране | редактиране на кода]Уравненията на Айнщайн описват как напрегнатостта на енергията (stress-energy) предизвиква изкривяване на пространството/времето.
Записани в тензорна форма те са
- където е тензор на Айнщайн, е тензор на напрегнатостта на енергията и е константа. Тензорите и са симетрични тензори от втори ранг. Те могат да бъдат записани като матрици от четвърти ред.
Решението на Уравненията на Айнщаин за полето ни дава метрика за времепространството. Тази метрика описва структурата на времепространството, зададена от напрегнатостта на енергията и съответната координатна система, за която е получено конкретното решение. Това са нелинейни диференциални уравнения и точното им решение често пъти е невъзможно. Все пак известни са множество частни решения.
Уравненията на Айнщайн за полето се свеждат към Законите на Нютон в случаите на слабо гравитационно поле и при скорости, много по-ниски от скоростта на светлината. При тези 2 приближения стойността на се определя от формулата:
Съществуват и други теории, обосновани на същите начални предположения, но включващи други ограничения. Резултатът почти винаги се изразява в друго уравнение за полето. Виж уравнения на Brans-Dicke, teleparallelism, теория на Rosen и теория на Einstein-Cartan.
Енергия, материя и изкривяване на времепространството
[редактиране | редактиране на кода]До тук имаме само бегла представа за уравненията на Айнщайн: G=8πT. От лявата страна G представлява тензор на Айнщайн. Този тензор от своя страна представлява геометрията на времепространството.
А от друга страна ние вече знаем че изкривяването на времепространството става при наличие на материя, това значи че Т от дясната страна на равенството е представянето на материята.
Тензорът Т (напрегнатост на енергията) се представя чрез следните серии от числа:
Txx, Txy, Txz, Txt, Tyy, Tyz, Tyt, Tzz, Tzt, Ttt;
Тези числа сами по себе си имат различен смисъл, заедно те представляват тензора на напрегнатост на енергията.
Метрика на Айнщайн относно изкривяване на пространството
[редактиране | редактиране на кода]Когато разглеждаме изкривяванията в пространството имаме нужда от специална метрика (измерителни единици) по подобие на:
, където:
d – разстояние между центъра на координатната система и дадена точка с координати x, y. Този запис е в сила когато x и y са разстояния, измерени спрямо единични вектори по координатните оси X и Y.
В случай че базовите вектори не са с единична дължина е необходимо да се направи корекция. По-точната формула за записване на горното разстояние е следната:
, където
- са коефициенти на пропорционалност по съответните координатни оси.
Вижда се че записа по този начин води до усложнения и затова прибягваме до по-опростено записване:
- ,
където:
Формулата за разстояние може да бъде обобщена и за наклонена координатна система (където осите X и Y не са перпендикулярни.
Така получените коефициенти са много важни във физиката. Заедно те определят метриката или физическото разстояние спрямо произволно избрана координатна система. В действителност метриката е още по-сложна от примера, който даваме. За да стане ясно това, е нужно да въведем и третата координата – Z и съответната метрика, свързана със Z: gzz, gxz, gyz. Трябва да въведем и времевата компонента на пространството: t и свързаните с нея метрични компоненти: gtt, gtx, gty, gtz.
Така получаваме 10 компоненти на пространството: gxx, gxy, gxz, gxt, gyy, gyz, gyt, gzz, gzt, gtt.
Метриката на пространството може да се променя при преминаване от една точка на пространството в друга. Ако работим с изкривена координатна система може да имаме координатна равнина, която започва в едно направление, но на друго място завършва сливайки се с координатната равнина от друго направление.
Възможно е да начертаем изкривена решетка върху плосък лист хартия. По такъв начин показваме метриката на изкривеното пространство, проектирайки го върху плоското пространство.
А от друга страна е невъзможно да начертаем идеална права линия върху изкривена плоскост.
Изследвайки много внимателно изменението на пространствената метрика от точка в точка можем да определим дали чертаем криволинейни координати в плоско пространство или чертаем в изкривено пространство.
Елементи на тензора напрегнатост-енергия
[редактиране | редактиране на кода](Stress-Energy Tensor)
Ttt – измерва количеството материя в дадена точка – плътност
Txt, Tyt и Tzt – измерва колко бързо масата се придвижва (импулс)
Txx, Tyy и Tzz – измерва напрегнатостта (налягането) по всяко едно от трите направления
Txy, Txz и Tyz – измерва напрегнатостта (усукването) на материята по координатните оси
Както се вижда от по-горе напрегнатостта, (налягане и усукване) и импулса влизат едновременно в Айнщайновото уравнение за полето. Това значи че напрегнатостта, (налягане, усукване) и импулс имат еднакво влияние върху изкривяването на времепространството. Това е свързано с другото известно уравнение на Айнщайн:
- – показващо че енергията има маса.
Изкривяването на времепространството засяга посоката на движение на телата и променя геодезията на пространството. В същото време уравнението на Айнщайн показва как материята и нейното движение или напрегнатост променят формата на времепространството. По този начин Айнщайн дава принципно решение на фундаменталните проблеми на физиката. Но в същото време намирането на практическите решения за конкретните ситуации се оказва доста трудно и си остава до голяма степен работа само за компютрите.
Вижте също
[редактиране | редактиране на кода]Външни препратки
[редактиране | редактиране на кода]- Describing How Mass Warps Spacetime Архив на оригинала от 2014-05-30 в Wayback Machine. – Уравнения на Айнщайн














