Котирана проекция

Котирана проекция е проекция, в която проекционната равнина (например означена с μ) винаги считаме за хоризонтална. На всяка точка А от пространството съпоставяме нейната ортогонална проекция А₁ в μ. За да се осигури еднозначно обратимо съответствие между точките в пространството и образите им, то след всяка точка в скоби се поставя разстоянието ѝ до проекционната равнина. То се взема със знак „+“, ако точката се намира над проекционната равнина, и със знак „-“, ако точката се намира под нея. Тези числа се наричат коти на точките, откъдето идва и името на този вид проекция.

Изобразяване на точка, права и равнина

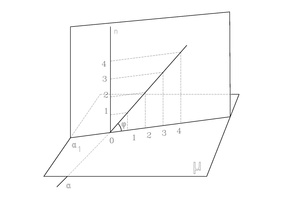
Точката, в която права пресича проекционната равнина, се нарича пробод или стъпка на правата. Правата, в която дадена равнина пресича проекционната равнина, се нарича диря или следа.
Една права е определена, ако са известни две нейни точки. В котирана проекция е прието правата да се изобразява с правоъгълната си проекцията в проекционната равнина, на която са отбелязани точките от правата с цели коти. Такава проекция се нарича градуирана проекция. За да се изясни получаването на градуирана проекция на правата се взима права а в пространството и нека О е прободът (стъпката) ѝ с проекционната равнина µ. От точката О издигаме перпендикуляр n към µ. по правата n нанасяме точките с коти цели числа: 1,2,3..., и при тези точки построяваме прави, успоредни на µ и лежащи в проектиращата равнина на правата а. Пресечните точки на тези прави с правата а са точки с цели коти 1,2,3,... Проекциите на последните точки в µ са точки от проекцията а1 на правата а. Те именно определят градуираната проекция на правата а.

Получените по този начин последователни точки върху правата а1 са на равни разстояния една от друга. Следователно е достатъчно да знаем две точки от проекцията с последователни коти и можем да градуираме цялата права. Големината на отсечката между проекциите на две точки с разлика между котите единица се нарича интервал на правата а. Интервалът i е функция на ъгъла ϕ, който правата а сключва с проекцията си (или все едно – с проекционната равнина), $i=\cot \phi$. Числото $p=\tan(\phi )$ се нарича наклон на правата а. Следователно $\pi =1$, т.е. интервалът и наклонът на една права са реципрочни величини. Когато наклонът расте от 0 до +∞ (т.е. ϕ расте от 0 до 90°), интервалът намалява от +∞ до 0.

Фигура 2. Главни и стръмни прави на равнината α

Ако една права е определена с две свои точки с цели координати, лесно я градуираме. Например ако правата е зададена с точките си А(3) и В(6), е достатъчно е да разделим отсечката А1В1 на три равни части. Ако познаваме две точки с дробни коти, ще разделяме отсечката между проекциите на повече части.

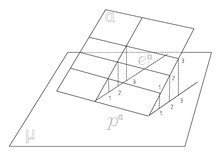
Нека е дадена равнина α, която не е успоредна на µ. Означаваме с p α пресечницата на α и µ, т.е. дирята на равнината α. Правите от равнината α, които са успоредни на p α се наричат хоризонтални или главни прави на α. Очевидно техните проекции са успоредни помежду си и на дирята. Важно е да се обърне внимание, че всички точки от една хоризонтална права имат равни коти.

Правите на равнината α, които са перпендикулярни на дирята, се наричат стръмни прави на α. От теоремата за трите перпендикуляра следва, че техните проекции са също перпендикулярни на дирята. Ясно е, че ъгълът между стръмна права и µ всъщност е ъгъл между равнината µ и α. Той се нарича ъгъл на наклона на равнината α. Градуираната проекция на стръмна права се нарича еталон на равнината. Когато е даден еталонът, равнината е напълно определена (ако познаваме еталона, можем да построим всяка хоризонтала на равнината). Прието е равнината да се изразява с еталона си.

Взаимни положения на точка права и равнина

Точка и права

Ако една точка А не лежи на дадена права а, в общия случай нейната проекция не лежи на проекцията на правата. Ако точката и правата лежат на една и съща проектираща равнина, то проекцията на точката лежи върху проекцията на правата, но котата на точката може да не е равна на котата на онази точка от правата, която има същата проекция. Тогава точката не лежи на правата. На картинката се вижда, че правата лежи на една и съща проектираща равнина, точката лежи върху проекцията на правата.котата на точката може да не е равна на котата на точката от правата.

Котирана проекция на права и точки

Две прави

Правите (обозначени като a и b) се пресичат

Тогава техните проекции също се пресичат или съвпадат

В първия случай пресечената точка на проекцията има една и съща кота спрямо двете прави.

Във втория случай двете прави имат обща проектираща равнина q.

Ако двете прави са успоредни, то техните проекции са успоредни. Ако двете прави са кръстосани, те не отговарят на условията за успоредност и за пресичане. Ако проекциите са успоредни, то те са разнопосочно градуирани или интервалите им не са равни.

Ако двете прави са кръстосани, те не отговарят на условията за успоредност и за пресичане. Именно ако проекциите им се пресичат, пресечната точка има различни коти спрямо двете прави. Ако проекциите са успоредни, то те са разнопосочно градуирани или интервалите им не са равни.

Точка и равнина

Едно достатъчно условие, точка да лежи в равнинае тя да лежи на правата от равнината. Поради това точка с кота n лежи на равнината, ако лежи на хоризонталата с кота n. Така точка (А) на фиг.лежи на равнината a докато (B) не лежи на a.

Инцидентност и успоредност на права и равнина

Една права може да лежи в равнина, да е успоредна на равнината или да я пробожда.

Права a лежи в равнина a, ако поне две нейни точки лежат в a. При това очевидно ако a не е хоризонтала за равнина, тя пресича хоризонталите с цели коти в точки със същите цели коти.

Инцидентност и успоредност на две равнини

Две равнини могат да се сливат, да са успоредни или да се пресичат. Ако се сливат, дирите им, стръмните им прави и хоризонталите им съвпадат. Ако са успоредни те имат успоредни дири, стръмни прави и хоризонтали. Еталоните им са две успоредни прави с равни интервали и са еднопосочно градуирани.

Пресечница на две равнини

Като всяка права, пресечницата на две равнини е напълно определена, ако са известни две нейни точки. Като търсим пресечницата на две равнини е достатъчно да намерим две различни точки, които лежат и на двете дадени равнини. Ако една равнина е успоредна на проекционната равнина, тч пресича двете дадени равнини в едноименни хоризонтали. Поради това общата точка на тези хоризонтали ще е точка от търсената пресечница. Такава точка можем да намерим, като пресечем двете дадени равнини с трета равнина, етанолът на която не е успореден на еталоните на двете дадени равнини. Пресечниците на тази трета равнина с дадените се пресичат в точка от пресечниците на дадените.

Пробод на права с равнина

Пробод на права с равнина изобразяваме, като вземем произволна спомагателна равнина, минаваща през дадената права и намерим нейната пресечница с дадената равнина. Търсеният пробод е точката, в която се пресичат намерената пресечница и дадената права, По този начин е намерен прободът S на права a с равнина a. Тук е взета спомагателна равнина (сигма), съдържаща правата a по-точно построени са две нейни хоризонтали. Свободата на избора на (сигма) тук се изразява в произволния избор на тези хоризонтали h σ (2) è h σ (5). Двойките хоризонтали h α (2), h β (2) è h α (5), h β (5) се пресичат в точки A и B съответно. Правата a и пресечницата s ασ = AB на a и σ лежат в помощната равнина σ и се пресичат в търсения пробод S.

Права, перпендикулярна на равнина

Както знаем от стереометрията, права е перпендикулярна на равнина, ако е перпендикулярна на поне две неуспоредни прави от равнината. От това следва, че правата е перпендикулярна на всяка права в равнината.

Права е перпендикулярна на равнина, когато са изпълнени следните условия:

1. проекцията и е успоредна, на еталона на равнината
2. интервалът ѝ е реципрочен на интервала на еталона
3. градуирането ѝ е разнопосочно на градуирането на еталона