Закон на Снелиус

Пречупване на лъч светлина на границата между две среди с различни коефициенти на пречупване.

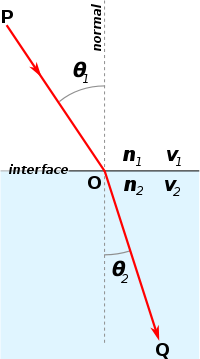
Законът на Снелиус описва пречупването на светлината на границата между две прозрачни среди. Приложим е и за описване на пречупването на вълни от друго естество, например звукови или радиовълни. Законът е открит през 1621 г. от холандския математик Вилеброрд Снелиус. Малко по-късно, през XVII век, е публикуван от Рене Декарт.

Ъгълът на падане $\theta _{1}$на светлината върху повърхността е свързан с ъгъла на пречупване $\theta _{2}$чрез съотношението

${\frac {\sin \theta _{1}}{\sin \theta _{2}}}={\frac {v_{1}}{v_{2}}}={\frac {n_{2}}{n_{1}}}$.

Тук $v_{1}$и $v_{2}$са скоростите на светлината съответно в първата и втората среда, а $n_{1}$ и $n_{2}$ са коефициентите на пречупване, които са в права зависимост от относителните диелектрични проницаемости на средите: $n_{1}={\sqrt {\varepsilon '_{1}}}$ и $n_{2}={\sqrt {\varepsilon '_{2}}}$. Законът може да бъде записан и във вида

$n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}$.

Отношението на скоростта на светлината в първата среда към скоростта на светлината във втората среда се нарича относителен коефициент на пречупване на втората среда спрямо първата.

Законът на Снелиус гласи:

Отношението на синусите на ъглите на падане и пречупване на електромагнитна вълна на разделната повърхност между две среди е равно на отношението на съответните скорости на вълната в тях и обратно пропорционално на отношението на техните коефициенти на пречупване.

Или:

Произведението на синуса на ъгъла на падане на електромагнитна вълна на разделната повърхност между две среди и коефициента на пречупване на първата среда е равно на произведението на синуса на ъгъла на пречупване и коефициента на пречупване на втората среда.

В контекста на закона на Снелус долната област е по-висок коефициент на пречупване и пропорционално по-ниска скорост на вълната от горната област. Вълновият фронт се променя и остава перпендикулярен на посоката на вълната (с червена линия).

Този закон следва от принципа на Ферма за най-краткото време.

Съществуват някои особености:

• В случай на анизотропни среди (например кристали със слаба симетрия или механически деформирани твърди тела) пречупването се подчинява на някои по-сложни закони. При това е възможна зависимост на посоката на пречупения лъч не само от посоката на падащия, но и от неговата поляризация.
• Законът на Снелиус не описва съотношението на интензивността и поляризацията на лъчите. За случаи като този се прилагат по-детайлните формули на Френел.
• Законът на Снелиус е добре определен за случая на геометрична оптика, тоест тогава, когато дължината на вълната е достатъчно малка в сравнение с размера на пречупващата повърхност.

Пълно вътрешно отражение

Ако първата среда е по-плътна от втората, тя е с по-голяма диелектрична проницаемост $\varepsilon _{1}>\varepsilon _{2}$ и $n_{1}>n_{2}$. От формулата за закона на Снелиус следва, че за да се запази равенството, $\sin \theta _{2}>\sin \theta _{1}$ и $\theta _{2}>\theta _{1}$. С увеличаване на ъгъла на падане при някаква негова критична стойност $\theta _{1kp}<90^{\circ }$ ъгълът на пречупване достига стойност $\theta _{2}=90$° и вълната се отразява от граничната повърхност, като се разпространява успоредно на нея:

Пречупване и отражение на светлината на границата между две среди.

Демонстрация на липса на пречупване при ъгли, по-големи от критичния ъгъл.

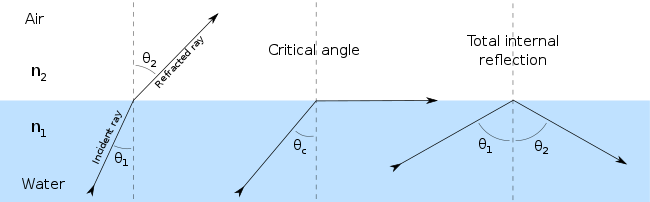
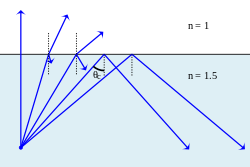
${\frac {\sin \theta _{1kp}}{\sin 90^{\circ }}}={\frac {n_{2}}{n_{1}}}$, откъдето $\theta _{1kp}=\arcsin {\frac {n_{2}}{n_{1}}}$.

При ъгъл на падане, по-голям от критичния, възниква пълно вътрешно отражение – отсъства пречупен лъч, а падащият лъч е напълно отразен от границата на средите. Условието за пълно вътрешно отражение може се определи от изложените изрази при известни коефициенти на пречупване или относителни диелектрични проницаемости на двете среди:

$\theta _{1}>\arcsin {\frac {n_{2}}{n_{1}}}$ или

$\theta _{1}>\arcsin {\sqrt {\frac {\varepsilon '_{2}}{\varepsilon '_{1}}}}$.

То може да се получи и от математическото изразяване на отсъствието на пречупена вълна: тя не съществува, когато $\sin \theta _{2}={\frac {n_{1}}{n_{2}}}\sin \theta _{1}>1$, или $\sin \theta _{1}>{\frac {n_{2}}{n_{1}}}$.

Векторна формула

Нека ${\vec {v}}_{1}$ и ${\vec {v}}_{2}$ са лъчеви вектори на падащия и пречупения лъч, т. е. вектори, указващи посоката на лъча и имащи дължини съответно $|{\vec {v}}_{1}|=n_{1}$ и $|{\vec {v}}_{2}|=n_{2}$. Нека ${\vec {n}}$ е единичен нормален вектор към пречупващата повърхност. Тогава е в сила формулата

${\vec {v}}_{2}={\vec {v}}_{1}+\left({\sqrt {{\frac {n_{2}^{2}-n_{1}^{2}}{({\vec {v}}_{1}\cdot {\vec {n}})^{2}}}+1}}-1\right)({\vec {v}}_{1}\cdot {\vec {n}}){\vec {n}}$.

Извеждане на формулата

Извеждане от принципа на Ферма

Законът на Снелиус може да бъде извлечен от принципа на Ферма, който гласи, че светлината изминава пътя, който отнема най-малко време. Като се вземе производната на дължината на оптичния път, стационарната точка се намира, давайки пътя, изминат от светлината. (Има ситуации, когато светлината нарушава принципа на Ферма, като не поема най-малкото времево разстояние, както при отражение в /сферично/ огледало.)

Както е показано на фигурата вдясно, светлината от точка Q на среда 1 навлиза през точка O в среда 2, възниква пречупване и накрая достига точка P. Скоростите на светлината в средите 1 и 2 са $v_{1}=c/n_{1}$ и $v_{2}=c/n_{2}$. Нека T е времето, необходимо на светлината да измине пътя QOP:

$T={\frac {\sqrt {x^{2}+a^{2}}}{v_{1}}}+{\frac {\sqrt {b^{2}+(l-x)^{2}}}{v_{2}}}={\frac {\sqrt {x^{2}+a^{2}}}{v_{1}}}+{\frac {\sqrt {b^{2}+l^{2}-2lx+x^{2}}}{v_{2}}},$

където $a,b,l$ и $x$ са както са означени на дясната фигура, като $x$ е променливият параметър.

Светлината от среда 1, точка Q, навлиза в среда 2, възниква пречупване и накрая достига точка P.

Времето T е минимално, когато първата му производна е нула:

${\frac {dT}{dx}}={\frac {x}{v_{1}{\sqrt {x^{2}+a^{2}}}}}+{\frac {-(l-x)}{v_{2}{\sqrt {(l-x)^{2}+b^{2}}}}}=0.$

От правоъгълните триъгълници с хипотенузи QO и OP следва, че

${\frac {x}{\sqrt {x^{2}+a^{2}}}}=\sin \theta _{1}$ и ${\frac {l-x}{\sqrt {(l-x)^{2}+b^{2}}}}=\sin \theta _{2}$

Следователно,

${\frac {dT}{dx}}={\frac {\sin \theta _{1}}{v_{1}}}-{\frac {\sin \theta _{2}}{v_{2}}}=0$

${\frac {\sin \theta _{1}}{v_{1}}}={\frac {\sin \theta _{2}}{v_{2}}}$

${\frac {n_{1}\sin \theta _{1}}{c}}={\frac {n_{2}\sin \theta _{2}}{c}}$

$n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}.$