Външен ъгъл
За информацията в тази статия или раздел не са посочени източници. Въпросната информация може да е непълна, неточна или изцяло невярна. Имайте предвид, че това може да стане причина за изтриването на цялата статия или раздел. |
Външният ъгъл е равен на разликата между 180° и вътрешния ъгъл. Може да приема стойности от 0° до 180°.
Дефиниция
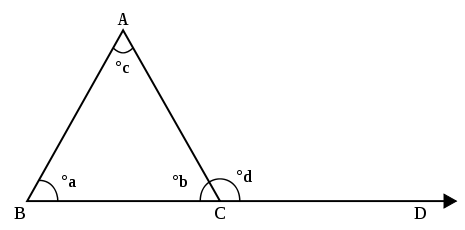
[редактиране | редактиране на кода]Ако продължим страната ВС на триъгълника АВС, както е на картинката, се получава ъгъл d, който е разположен извън триъгълника и е съседен на ъгъл b. Външен ъгъл на триъгълник се нарича съседният на кой да е вътрешен негов ъгъл.
Всеки ъгъл на триъгълника има по 2 съседни ъгъла. Следователно един триъгълник има шест външни ъгъла – 2 по 2 равни.
От свойство на съседни ъгли следва, че d = 1800 – b.
Теорема
[редактиране | редактиране на кода]Всеки външен ъгъл е равен на сбора на двата вътрешни, несъседни нему, ъгъла.
Доказателство:
От определението за външен ъгъл следва, че d = 1800 – b.
От сбор на ъгли в триъгълник следва, че a + b + c = 1800,
Следователно a + c = 1800 – b, но и d = 1800 – b.
Следователно a + c = d, което трябваше да докажем.
Следствие
[редактиране | редактиране на кода]Всеки външен ъгъл на триъгълника е по-голям от всеки вътрешен, несъседен нему, ъгъл от същия триъгълник.
Примерна задача
[редактиране | редактиране на кода]
Два от външните ъгли на триъгълник са 1100 и 1200. Намерете третия външен ъгъл и вътрешните ъгли на триъгълника.
Решение:
Нека α' е съседен на α и α' = 1800 – α = 1100. Следователно α = 700.
Аналогично β' е съседен на β и β' = 1800 – β. Следва, че β = 600.
Аналогично β' е съседен на β и β' = 180 – β. β = 60.
От сбор на ъгли в триъгълник следва, че α + β + γ = 1800.
Следователно γ = 1800 – 600 – 700 = 500.
Понеже γ е съседен на последния външен ъгъл γ' – следва че γ' = 1800 – γ = 1300.
От тази задача следва и че сборът на външните ъгли на триъгълника е равен на 3600, което важи и за всеки триъгълник.