Файл:Hyperbolic and exponential; cosh.svg
Облик
Размер на този PNG предварителен преглед на изходния SVG файл: 389 × 530 пиксела. Други разделителни способности: 176 × 240 пиксела | 352 × 480 пиксела | 564 × 768 пиксела | 751 × 1024 пиксела | 1503 × 2048 пиксела.
Оригинален файл (Файл във формат SVG, основен размер: 389 × 530 пиксела, големина на файла: 72 КБ)
История на файла
Избирането на дата/час ще покаже как е изглеждал файлът към онзи момент.
| Дата/Час | Миникартинка | Размер | Потребител | Коментар | |
|---|---|---|---|---|---|
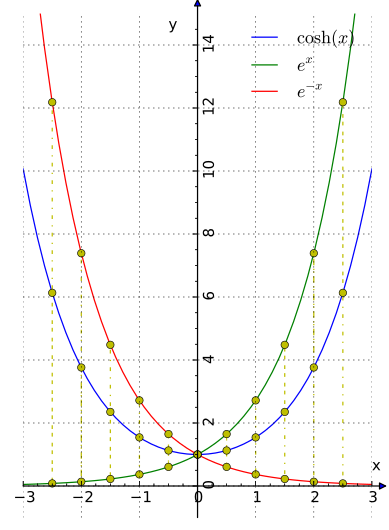
| текуща | 11:59, 4 юни 2011 |  | 389 × 530 (72 КБ) | Krishnavedala | {{Information |Description ={{en|1=Hyperbolic functions can be defined by exponential functions: {| |- | style="vertical-align:top;"|[[:File:Hyperbolic and exponential; cosh.png|thumb|300px|cosh(x) i |
Използване на файла
Следната страница използва следния файл:
Глобално използване на файл
Този файл се използва от следните други уикита:
- Употреба в ba.wikipedia.org
- Употреба в ca.wikipedia.org
- Употреба в cv.wikipedia.org
- Употреба в en.wikipedia.org
- Употреба в eu.wikipedia.org
- Употреба в hi.wikipedia.org
- Употреба в hy.wikipedia.org
- Употреба в id.wikipedia.org
- Употреба в mk.wikipedia.org
- Употреба в ro.wikipedia.org
- Употреба в ru.wikipedia.org
- Употреба в simple.wikipedia.org
- Употреба в sq.wikipedia.org
- Употреба в ta.wikipedia.org
- Употреба в tr.wikipedia.org
- Употреба в zh-min-nan.wikipedia.org



